I Like Pi
- 90
- 0
I know this has been asked before, but it was never really clearly explained.. The problem is as follows:
What is the acceleration of the system shown in the diagram if the kinetic coefficient of friction is 0.15?
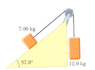
[diagram attached.. if not visible, it is an incline plane, with angle +37 deg. the box on the plane is 7 kg and it is being pulled upwards on the plane by a box 12 kg that is connected to a pulley going vertically down the side of the incline (it is a right angle triangle, of course)]
I related this to Atwood's machine as if it were vertical..
I know that the force on the m2 (12 kg box) is Fg2.
For the one on the incline, i just imagined it to be hanging vertically and pictured the forces acting downwards on it, which is Ff and Fg1.
Using Newton's second law, F = ma
I got -(Ff+Fg_{1})+Fg_{2}=(m_{1}+m_{2})a
therefore:
-[(mu)m_{1}g+m_{1}gsinx]+m_{2}g=(m_{1}+m_{2})a
From there on it's just plugging in the values, but I'm not so sure if I'm correct?
Thanks in advance!
Homework Statement
What is the acceleration of the system shown in the diagram if the kinetic coefficient of friction is 0.15?
[diagram attached.. if not visible, it is an incline plane, with angle +37 deg. the box on the plane is 7 kg and it is being pulled upwards on the plane by a box 12 kg that is connected to a pulley going vertically down the side of the incline (it is a right angle triangle, of course)]
Homework Equations
The Attempt at a Solution
I related this to Atwood's machine as if it were vertical..
I know that the force on the m2 (12 kg box) is Fg2.
For the one on the incline, i just imagined it to be hanging vertically and pictured the forces acting downwards on it, which is Ff and Fg1.
Using Newton's second law, F = ma
I got -(Ff+Fg_{1})+Fg_{2}=(m_{1}+m_{2})a
therefore:
-[(mu)m_{1}g+m_{1}gsinx]+m_{2}g=(m_{1}+m_{2})a
From there on it's just plugging in the values, but I'm not so sure if I'm correct?
Thanks in advance!
Attachments
Last edited: