Dave7000
- 8
- 1
- TL;DR
- Spindle position in scissor mechanism to achieve uniform movement.
Hello, regards to all.
I am designing a CNC machine where the table will work as a Z axis.
I have found a complication when trying to save space under the table, to avoid set the ballscrew upright I have decided to make a scissor mechanism but I have noticed that when the ballscrew travel 10mm, the table does not.
I placed the ballscrew in several positions, not in the center of the legs pin or totally horizontal to achieve the same travel between ballscrew and table height, or some fraction as half or 1/4 something that can be fixed later with the machine controller.
At first I thought it could be a mathematical problem of triangles. I'm not so sure anymore. After days trying I ask for help in this forum to save the scissor desing.
Can anybody help me?
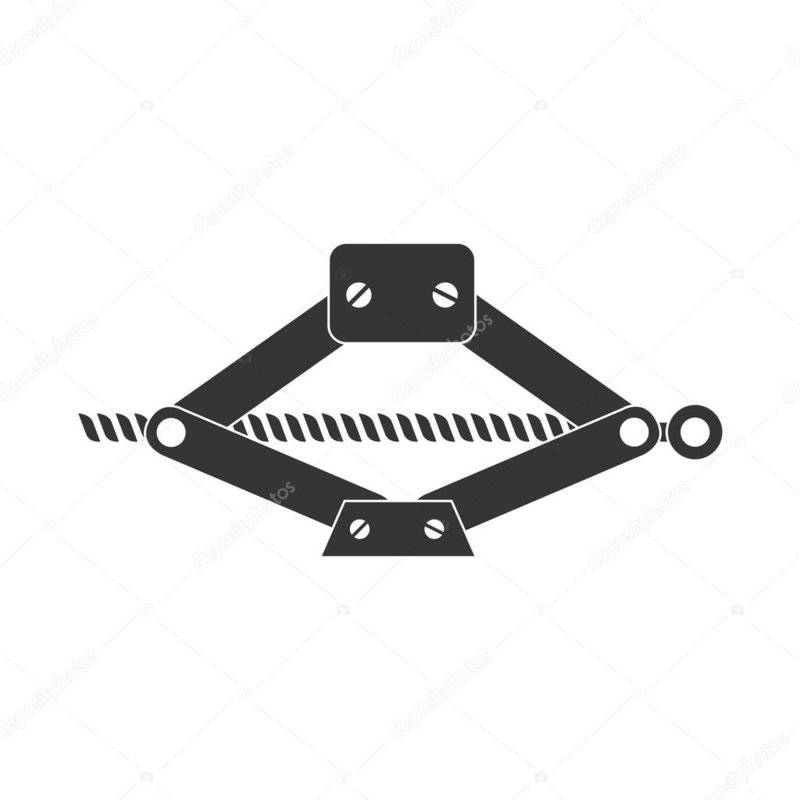
I am designing a CNC machine where the table will work as a Z axis.
I have found a complication when trying to save space under the table, to avoid set the ballscrew upright I have decided to make a scissor mechanism but I have noticed that when the ballscrew travel 10mm, the table does not.
I placed the ballscrew in several positions, not in the center of the legs pin or totally horizontal to achieve the same travel between ballscrew and table height, or some fraction as half or 1/4 something that can be fixed later with the machine controller.
At first I thought it could be a mathematical problem of triangles. I'm not so sure anymore. After days trying I ask for help in this forum to save the scissor desing.
Can anybody help me?
 !
!