Banking a Road: Calculating the Angle at 30ms^-1

[Identity]

Homework Statement

A road is to be banked so that any vehicle can take the bend at a speed of 30 ms^-1 without having to rely on sideways friction. The radius of the curvature of the road is 12m. At what angle should it be banked?

Homework Equations

various inclined slope equations...

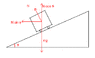
The Attempt at a Solution

I got

N\cos\theta = mg,

N\sin\theta = \frac{mv^2}{r},

so

\tan\theta = \frac{v^2}{gr}

\therefore \theta = 82.4^{\circ}

BUT, I have a question about this:

From a simple inclined slope, we have N = mg\cos\theta

So, mg\cos\theta\sin\theta = \frac{mv^2}{r}

But subbing in \theta = 82.4^{\circ} now doesn't work! How come??

 

[psykatic]

The free body diagram of a body moving on a road banked at certain angle \theta can be drawn as in the attachment.
In the attachment, consider the following things:
N-->Normal reaction exerted by the surface (perpendicularly) on the moving vehicle
mg--> weight of the body, acting downwards
N~cos\theta,~N~sin\theta--> components of N

As you can see, the downward force, i.e the weight of the body is balanced by the cos component of N (Normal Reaction), and thus it is,

N~cos\theta~=~mg

Also the centripetal force required by the vehicle to move in a circular orbit is provided by the sin component of N,

N~sin\theta~=~mv^2/r

Now that you know this, let me add, if you resolve 'mg', you'll certainly realize...