Bayes Networks - calculations in terms of joint distribution

[clobbasaurus]

Hi I am trying to calculate a particular problem from a given bayesian network.

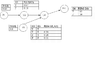
The network consists of nodes G1,G2,G3,G4,Pr1

G1 leads to G2, G2 leads to G4 and G3 also leads to G4 but it has no parents, and G4 leads to Pr1.

The probability tables for the nodes are:

P(G1) = 0.02
P(G2|G1) True = 0.67 False = 0.10
P(G3) = 0.6
P(G4|G2,G3) = G2True and G3True = 0.772, G2True and G3False = 0.70
G2False and G3True = 0.24, G2False and G3False = 0.01

P(Pr1|G4) = True 0.61 False 0.34

From this

I am trying to calculate P(Pr1|G1,¬G3)

I think I can do this by expressing in terms of components of the joint distribution, and calculating each of these from the network.

So far I have the formula

P(Pr1|G1,¬G3) = P(Pr1,G1,¬G3)/P(G1,¬G3)

P(Pr1,G1,¬G3) =
P(Pr1,G1,¬G3,G2,G4)+
P(Pr1,G1,¬G3,G2,¬G4)+
P(Pr1,G1,¬G3,¬G2,G4)+
P(Pr1,G1,¬G3,¬G2,¬G4)

As I already know the values for G1 and G3 this bit is ok, but how do I calculate the values for Pr1,G2 and G4 as I assume they have to be worked out from the values in the probability tables (or are the values already in the tables and am I just being Thick) . If you would like to see a picture of the bayes network, I have a .gif I can send. I have attached what I have done so far and the missing value from the probability table in the .gif is 0.772

Thanks a lot

Mike

 

[Enuma_Elish]

Suppose p denotes the unconditional Pr1. Then isn't P(Pr1,G1,¬G3) = p x 0.98 x 0.4?
Strike that; I need to think more.

 

[Architeuthis Dux]

Hello Mike,

Thank you for sharing your question and the work you have done so far. It seems like you are on the right track in terms of approaching this problem through the joint distribution. The formula you have for P(Pr1|G1,¬G3) is correct, and the next step is to calculate the values for Pr1, G2, and G4 using the probability tables provided.

To calculate the value for Pr1, you can use the given probability table for P(Pr1|G4). Since G4 is the only parent node for Pr1, you can use the values for G4 to determine the probability of Pr1 being True or False.

For G2 and G4, you can use the conditional probability table P(G4|G2,G3) to determine the values for G2True and G3False. From there, you can use the given values for P(G2|G1) and P(G3) to determine the remaining values for G2 and G4.

Once you have all the values for Pr1, G2, and G4, you can plug them into your formula for P(Pr1|G1,¬G3) and solve for the final probability.

I hope this helps and good luck with your calculations! If you have any further questions, please let me know.