Robin91
- 7
- 0
Homework Statement
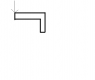
The problem is to determine the maximum deflection when a person is standing on the beam in the attachment.
E= 206.8 GPa, v=0.3
Homework Equations
The Attempt at a Solution
I've thought a bit about the problem, but I don't know exactly where to start. The beam is asymmetical, which implies that it will most likely bend into the negative z direction and twist a bit.
If you could steer me into the right direction it will be most appreciated!
Thanks,
Robin