Turbine
- 9
- 0
Hi guys,
Hopefully a fairly simple question. All beam formulas I've come across, whether in my own textbooks or Machinery's Handbook, have two sets of formulas for beams. One will be for "simply supported", where one end is pinned and the other end is a pin-roller. The other connection type is simply "fixed". Where would a beam connection fall among those which has ends that are both pinned without "rollers". Basically I'm analyzing a horizontal steel beam pinned between two vertical beams.
Example:
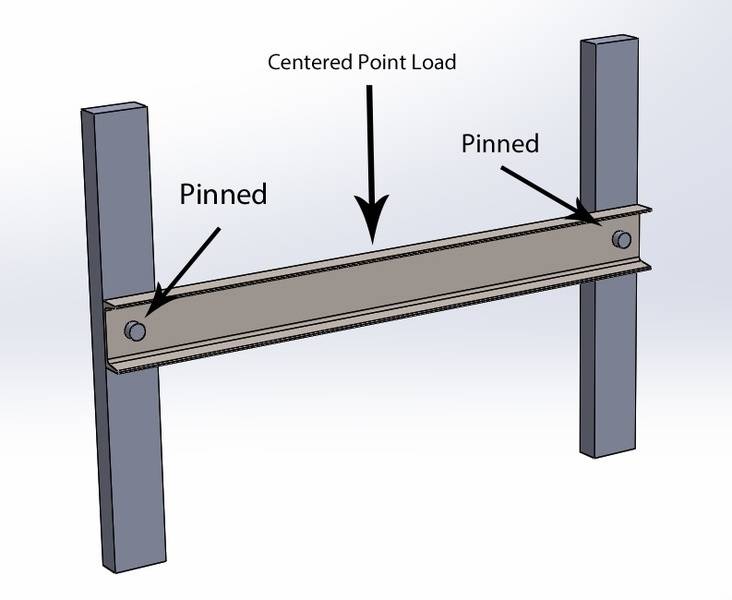
This very well is just a "simply supported" example, my only hesitation is knowing that there will be no horizontal translation in my design, whereas in traditionally "simply supported" situation, there is horiz. translation due to the the roller. Hopefully someone can set me straight. Thank you!
Hopefully a fairly simple question. All beam formulas I've come across, whether in my own textbooks or Machinery's Handbook, have two sets of formulas for beams. One will be for "simply supported", where one end is pinned and the other end is a pin-roller. The other connection type is simply "fixed". Where would a beam connection fall among those which has ends that are both pinned without "rollers". Basically I'm analyzing a horizontal steel beam pinned between two vertical beams.
Example:
This very well is just a "simply supported" example, my only hesitation is knowing that there will be no horizontal translation in my design, whereas in traditionally "simply supported" situation, there is horiz. translation due to the the roller. Hopefully someone can set me straight. Thank you!
Last edited: