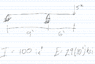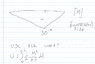Beam Deflection Using Work Methods

[stinlin]

Homework Statement

Find deflection at point of load application.

Homework Equations

See attached.

The Attempt at a Solution

I know the equation to use, but I have NO idea how to apply it here. Also - can't use virtual work. The problem explicitly states real work. How on Earth do I begin this? ^.^

 

[Mapes]

Your attachments aren't available for viewing yet, but the general strategy here is to equate work (applied force times deflection at point of load) and energy (total strain energy in the beam). Does this help?

 

[Pyrrhus]

Mapes gave the correct idea.

Basicly in linear elastic materials

W = \frac{P \delta}{2} = U = \int_{0}^{L} \frac{M^{2}dx}{2EI}

Of course if you notice due to the nature of the strain energy being quadratic function of the loads instead of being linear, it does not allow us to find the displacements for 2 or more loads acting on the structure. This is because we will have multiple unknowns and just 1 equation (the one above).

Your case is solvable by this method.