Beam problem finding max bending stress

AI Thread Summary
To find the maximum bending stress in a beam with a specified diameter, it is essential to incorporate the beam's diameter into the bending stress formula, which typically involves the moment of inertia. The diameter affects the moment of inertia, which in turn influences the calculated bending stress at the point of maximum moment. The bending moment diagrams remain the same, but the stress calculations will differ due to the beam's geometry. Understanding how to calculate bending stresses involves using the formula σ = M*c/I, where σ is the bending stress, M is the moment, c is the distance from the neutral axis to the outer fiber, and I is the moment of inertia. Therefore, the diameter is crucial for accurate stress calculations in beam analysis.
Resa
Messages
8
Reaction score
0
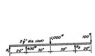
Alright so I drew it out like did the reactions and everything then I realized I need to include the diameter of the beam. How do I find the max bending stress while using the diameter of the beam? All I need to know is what exactly I do differently compared to drawing the bending moment diagrams with that 2 and 1/2 inch diameter.
 

Attachments

  • beam prob.png
    beam prob.png
    3.3 KB · Views: 576
Physics news on Phys.org
Without including I got R1 to be 50 and R2 to be 650..
 
Reactions look good. The diameter comes into play when calculating max stress at point of max moment. Why would the moments be different if the shaft was of a different diameter? Do you know how to calculate bending stresses?
 

Similar threads

Engineering Combined loading, where is the neutral axis?
Replies
11
Views
3K
Question about the location of max bending stress in a beam
Replies
2
Views
7K
Engineering Distance is a problem -- find shear force and bending moment diagram
Replies
2
Views
2K
Maximum and minimum tensile/compressive strain in beam
Replies
15
Views
6K
Max Bending Stress: Find from Second Moment of Area
Replies
3
Views
3K
Parallel Axis Theorem / Bending Stress
Replies
6
Views
3K
Finding the bending moment for maximum stress
Replies
6
Views
3K
Calculating the bending stress of a simply supported beam
Replies
5
Views
6K
Maximum Bending Stress in Cantilevered Steel Channel Beam
Replies
6
Views
2K
Yes, that is correct. Good job!
Replies
11
Views
4K

Hot Threads

Recent Insights

Back
Top