Khalid Qasim
- 2
- 0
Thread moved from the technical forums
Summary:: Bernoulli’s Equation and External Forces
Hello all, I am a bit confused on this question:
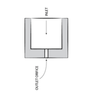
Water flows through a spray nozzle (as shown in the figure below) at a rate of 50 cm3 h -1 .
The internal inlet diameter of the nozzle entrance is 5 cm and the internal exit diameter of the nozzle is 1 cm.
The gauge pressure is 2.75 bar at the entrance of the nozzle and the pressure outside the nozzle exit is atmospheric.
Calculate the external force required to keep the spray nozzle in place, and the direction of this force.
State any assumptions you make and give all the steps in your calculation.
I have tried using bernoulli's eq to find different velocities to calculate momentums to hopefully find a thrust force, but to no avail. Can someone help?
Hello all, I am a bit confused on this question:
Water flows through a spray nozzle (as shown in the figure below) at a rate of 50 cm3 h -1 .
The internal inlet diameter of the nozzle entrance is 5 cm and the internal exit diameter of the nozzle is 1 cm.
The gauge pressure is 2.75 bar at the entrance of the nozzle and the pressure outside the nozzle exit is atmospheric.
Calculate the external force required to keep the spray nozzle in place, and the direction of this force.
State any assumptions you make and give all the steps in your calculation.
I have tried using bernoulli's eq to find different velocities to calculate momentums to hopefully find a thrust force, but to no avail. Can someone help?