howsockgothap
- 59
- 0
Biot-Savart Law-- magnetic field produced by single wire.
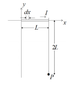
A wire of length L, carrying current I lies along the x-axis as shown in the picture. A
point P is located a distance 2L below the right end of the wire, as shown.
a) Determine the direction of the contribution dB to the magnetic field at P due to the
element dx of the wire.
b) Write an expression for the contribution, dB, to the magnetic field due to element dx.
c) Calculate the magnetic field B at point P due to the entire wire.
dB=μ0I|d\vec{s}x\hat{r}|/4πr2
This is study for an exam and as such my prof refuses to tell us whether or not our answers are wrong, since it doesn't help us learn or something, I DUNNO. I've done the problem as best I could but didn't finish because I'm almost 100% positive I'm doing something wrong but am not sure how to rectify the problem.
So far I have that looking at the image provided B would be facing into the page.
Then:
dB=μ0I|d\vec{s}x\hat{r}|/4πr2
with r2=((2L)2+x2) and |d\vec{s}x\hat{r}=sinθ=x/((2L)2+x2)1/2
I worked that down to:
dB=μ0Ixdx/4π((2L)2+x2)3/2
This is where I stopped. It seems to me that what I have so far doesn't seem to incorporate the y component at all except where (2L)2 is mentioned, but this isn't really like other problems I've done where dBy is negligible due to symmetry so I wondered if I was doing it wrong. Does this look correct so far?
EDIT: Solved on my own.
dB=μ0I|d\vec{s}x\hat{r}|/4πr2
with r2=((2L)2+x2) and |d\vec{s}x\hat{r}=sinθ=2L/((2L)2+x2)1/2
dB=μ0I2Ldx/4π((2L)2+x2)3/2
integrate from 0 to L...
dB=μ0I2L/4π * L/[2L2((2L)2+L2)1/2]
=μ0IL/[(2L)2+L2] where 2L=R
and if L<<R
then B= μ0I/4πR
Homework Statement
A wire of length L, carrying current I lies along the x-axis as shown in the picture. A
point P is located a distance 2L below the right end of the wire, as shown.
a) Determine the direction of the contribution dB to the magnetic field at P due to the
element dx of the wire.
b) Write an expression for the contribution, dB, to the magnetic field due to element dx.
c) Calculate the magnetic field B at point P due to the entire wire.
Homework Equations
dB=μ0I|d\vec{s}x\hat{r}|/4πr2
The Attempt at a Solution
This is study for an exam and as such my prof refuses to tell us whether or not our answers are wrong, since it doesn't help us learn or something, I DUNNO. I've done the problem as best I could but didn't finish because I'm almost 100% positive I'm doing something wrong but am not sure how to rectify the problem.
So far I have that looking at the image provided B would be facing into the page.
Then:
dB=μ0I|d\vec{s}x\hat{r}|/4πr2
with r2=((2L)2+x2) and |d\vec{s}x\hat{r}=sinθ=x/((2L)2+x2)1/2
I worked that down to:
dB=μ0Ixdx/4π((2L)2+x2)3/2
This is where I stopped. It seems to me that what I have so far doesn't seem to incorporate the y component at all except where (2L)2 is mentioned, but this isn't really like other problems I've done where dBy is negligible due to symmetry so I wondered if I was doing it wrong. Does this look correct so far?
EDIT: Solved on my own.
dB=μ0I|d\vec{s}x\hat{r}|/4πr2
with r2=((2L)2+x2) and |d\vec{s}x\hat{r}=sinθ=2L/((2L)2+x2)1/2
dB=μ0I2Ldx/4π((2L)2+x2)3/2
integrate from 0 to L...
dB=μ0I2L/4π * L/[2L2((2L)2+L2)1/2]
=μ0IL/[(2L)2+L2] where 2L=R
and if L<<R
then B= μ0I/4πR
Attachments
Last edited: