Vibhor
- 971
- 40
Homework Statement
What is the relationship between " acceleration of block with respect to wedge" and "acceleration of wedge " ?
Homework Equations
The Attempt at a Solution
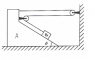
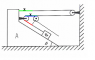
If the wedge moves by x units , then the string gets loosened/shortened at three places . The top two are x units .The last one in red is xcosθ .The total effect is the block moves down by a distance (2 + cosθ)x .
So, if acceleration of the wedge is 'a' then acceleration of block with respect to wedge aB,W = (2+cosθ)a .
But , this is incorrect .
Where am I getting it wrong ?
Many Thanks