Block up an incline and then how far it goes. HARD

[kerbyjonsonjr]

Homework Statement

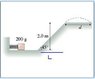
The spring in the figure has a spring constant of 1300 N/m . It is compressed 13.0cm , then launches a 200g block. The horizontal surface is frictionless, but the block's coefficient of kinetic friction on the incline is 0.180.

What distance does the block sail through the air?

Homework Equations

U=1/2kx²
KE=1/2mv²
U=mgh
V=v +at
x=vt +1/2at²

The Attempt at a Solution

This problem really is a pain. My teacher told me that at the bottom the only energy is the spring which is 1/2kx² At the top is there is kinetic energy and gravitational potential energy and the work done by the friction. So, 1/2mv² +mgh - f_k * L
To find the force of friction I drew a free body diagram and solved that out and got f_k=.249
I use trig to find out the height and the length of the triangle and got 1.41
Then I just plugged in all of the numbers. I got 10.985 for the potential spring energy and set that equal to the above equation so I had. 10.985=.5*.2*v²+.2*9.81*1.41 -.249*1.41
Solved that for v and got v=9.26 m/s
Then I found the y component of that and got 6.55 and plugged that into v=v +at so 0=6.55 + (-9.81)t so t=.67s
Since acceleration in the x direction is 0 I just plugged that into x=vt and got 4.37 but that answer is wrong.
I have no idea where I went wrong. There are so many steps in this problem. I think it could be because v^f does not equal zero so my equation v=v +at is wrong but I am not sure. I do not know what v_f would be if it is not 0. I would really appreciate any help. Thanks!

 

[Salamon]

Do you know the angle of the incline?

Here is one of the mistakes you made. At the top of the incline, the block has no Kinetic Energy since it has come to rest.

The elastic potential energy which you can and did calculate using U = 1/2 kx^2 is converted into KE while the block moves on the frictionless horizontal surface (BEFORE the block begins to move up the incline). This kinetic energy is lost as the block moves up the incline due to an increase in gravitational potential energy and work done against friction.


So
1/2kx^2 = mgh + .180(mg cosx)L

or using trig we can express h as Lsinx since sinx=h/L


Giving us
1/2kx^2 = mgL(sinx) + .180(mg cosx)L


If you know angle x of the incline, I think you can solve this.

 

[kerbyjonsonjr]

Do you know the angle of the incline?

Here is one of the mistakes you made. At the top of the incline, the block has no Kinetic Energy since it has come to rest.

The elastic potential energy which you can and did calculate using U = 1/2 kx^2 is converted into KE while the block moves on the frictionless horizontal surface (BEFORE the block begins to move up the incline). This kinetic energy is lost as the block moves up the incline due to an increase in gravitational potential energy and work done against friction.


So
1/2kx^2 = mgh + .180(mg cosx)L

or using trig we can express h as Lsinx since sinx=h/L


Giving us
1/2kx^2 = mgL(sinx) + .180(mg cosx)L


If you know angle x of the incline, I think you can solve this.

If you look at the picture in the attachment you will see that the box keeps moving after it goes up the incline and then it becomes a trajectory problem.