photon184739
- 3
- 0
In satellite motion around a planet, if the satellite is in orbit, it experiences only the gravitational force and its energy in orbit is constant (see 'https://openstax.org/books/university-physics-volume-1/pages/13-4-satellite-orbits-and-energy'):
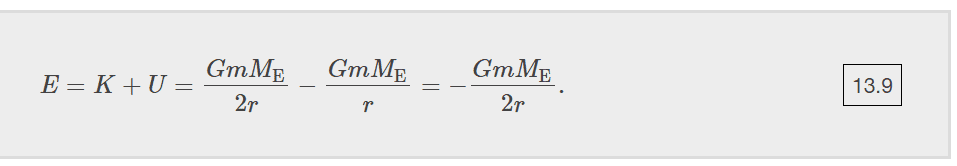
It's not radiating energy, is it? Its total energy is constant and a function of 'r' only, which is constant.
It's not radiating energy, is it? Its total energy is constant and a function of 'r' only, which is constant.