gamitor
- 9
- 0
Dear all,
How can I show that:
The boundary of a set S is equal to the intersection of the closure and the closure of the complement of S ?
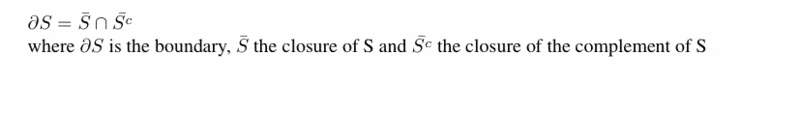
Thanks a lot in advance
How can I show that:
The boundary of a set S is equal to the intersection of the closure and the closure of the complement of S ?
Thanks a lot in advance