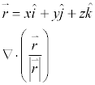Calculate Dot Product of Nabla and Vector | Partial Derivative Method

[dalarev]

[SOLVED] Divergence, nabla

Homework Statement

Given the vector, find the dot product.

Homework Equations

dot product of nabla and the vector is just partial derivative of each component.

The Attempt at a Solution

I'm trying to figure out if I can just leave out the denominator, since it is a scalar (the magnitude of vector r). The answer, however, is 2/r , so I'm starting to think it's going to be necessary to change to plane polar coordinates.

 

[HallsofIvy]

While the denominator is a scalar, it is still a function of x, y, and z. No, you certainly cannot leave it out. You could write the vector as
\left(\frac{x}{\sqrt{x^2+ y^+ z^2}}, \frac{y}{\sqrt{x^2+ y^+ z^2}},\frac{z}{\sqrt{x^2+ y^+ z^2}}\right)
and differentiate the three components of that with respect to x, y, and z, respectively and then add.

While the vector might be simpler in polar coordinates, you would also have to rewrite the operator in polar coordinates- and that is not trivial. Differentiating with respect to x, y, and z is not that difficult. Just write the first component as x(x^2+ y^2+ z^2)^{1/2} and differentiate with respect to x. You can then use "symmetry" to just write down the other derivatives, swapping the coordinates as appropriate.

 

[dalarev]

While the denominator is a scalar, it is still a function of x, y, and z. No, you certainly cannot leave it out. You could write the vector as
\left(\frac{x}{\sqrt{x^2+ y^+ z^2}}, \frac{y}{\sqrt{x^2+ y^+ z^2}},\frac{z}{\sqrt{x^2+ y^+ z^2}}\right)
and differentiate the three components of that with respect to x, y, and z, respectively and then add.

While the vector might be simpler in polar coordinates, you would also have to rewrite the operator in polar coordinates- and that is not trivial. Differentiating with respect to x, y, and z is not that difficult. Just write the first component as x(x^2+ y^2+ z^2)^{1/2} and differentiate with respect to x. You can then use "symmetry" to just write down the other derivatives, swapping the coordinates as appropriate.

Thank you for that, exactly what I needed. The rest is just repetitive differentiation, thanks for the help. /solved