Calculate Minor Losses due to Flow Geometry Alone

[Timtam]

Hi does anyone know a way to calculate the Minor losses related just to flow Geometry isolated from Major frictional losses, all the k tables I can find combine the frictional losses with the geometry losses eg see below blurb from

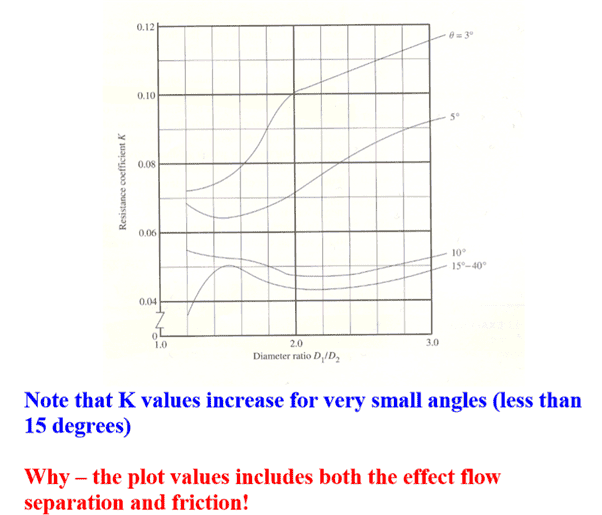
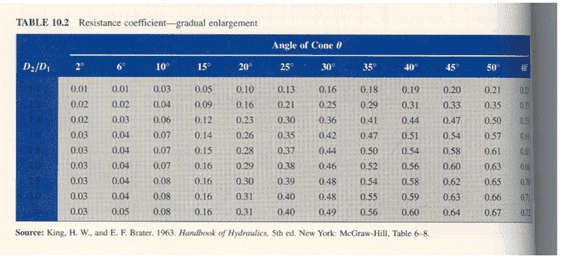
but I was hoping to obtain a first principles formula that could equate these losses solely to area and velocity change

The reason being is I am assuming that major losses component of the K values must be based on particular viscosity fluid but I would like to calculate this for different viscosity fluids ?

Also for the Darcy Weisbach if I want to calculate just the frictional losses would I use the average diameter of a convergent or divergent section of pipe ?

If such a formula exists it ok to just plain add these two effects ?

Am I making life to difficult for myself is there an easier way ?

 

[boneh3ad]

There's really nothing about these sorts of head loss calculations that comes from first principles. It is basically all empirical.

But here is a more fundamental issue: if there was no viscosity at all, what do you think would cause such losses to occur in these sorts of situations?

 

[Timtam]

This is what confuses me. I always thought that minor losses are (like major head loss ) also proportional to the viscosity of the fluid but I am seeing statements like the below that suggest that it isn't.

where KL means (local) loss coefficient. Although KL is dimensionless, it is not correlated in the literature with the Reynolds number and roughness ratio but rather simply with the raw size of the pipe.

In an inviscid flow I was assuming that these Minor head losses come from the force required to change the Momentum of the flow or the orthogonal area the obstruction presents to the flow.

That said it makes sense to me that a lower viscosity fluid would find it easier to change direction and thus would incur smaller later flow separation

Is this correct ? could I also reduce my Minor head loss ( as well as my Major head loss) by using a lower viscosity fluid ?

 

[boneh3ad]

The broader point I was trying to make is that an inviscid flow would incur no losses. Separation doesn't really make sense as a concept without viscosity. So, there is no source of dissipation to cause losses in an inviscid flow. Sure a force is required to accelerate the flow through a contraction, but that comes from a pressure gradient, and that pressure gradient is completely reversible in an inviscid flow. It's basically Bernoulli's equation.