javii
- 23
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
Is it correct?
No. You need to use the moment of inertia about the corner of the carton and you need to find the correct height of the center of mass when tipping occurs.javii said:Is it correct?
That is true, but since no mention is made in the problem about liquid in the carton, we may assume that it is empty. It could an empty carton on a cafeteria conveyor belt on its way to the trash disposal area.berkeman said:The movement of the liquid inside the carton would need to be accounted for in a full solution, IMO.
It's also an issue for cartons that are full. The milk would tend to rotate internally in the opposite direction.berkeman said:Maybe this problem does not intend to involve the full complexity of this situation, but milk cartons are not "full" of liquid, even when new. The movement of the liquid inside the carton would need to be accounted for in a full solution, IMO.
So, the formula i have to use is:kuruman said:No. You need to use the moment of inertia about the corner of the carton and you need to find the correct height of the center of mass when tipping occurs.
Why are you dividing the 0.195 by 2 but not the 0.07?javii said:So, the formula i have to use is:
1/3*m*(b^2+l^2)?
and when i use that one i get
View attachment 196008
And why do you think the CM is at height ##\frac{0.195}{2}~m## just before the carton tips over? That's its height when the carton sits flat on the conveyor belt.javii said:which leads me to:
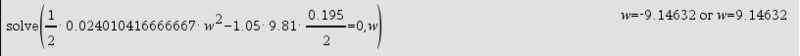
For me, it is obvious that I have to divide 0.195 with 2, but I am not sure if 0.07 also have to be divided with 2 since the carton isharuspex said:Why are you dividing the 0.195 by 2 but not the 0.07?
Yes, but it is important to understand why. Start with ##I_{CM}=\frac{1}{12}M(l^2+a^2)## and apply the parallel axes theorem. Try using symbols, not numbers. What do you get?javii said:So your are saying, that I also have to divide 0.07 with 2?
kuruman said:Yes, but it is important to understand why. Start with ##I_{CM}=\frac{1}{12}M(l^2+a^2)## and apply the parallel axes theorem. Try using symbols, not numbers. What do you get?
I see, it is a mistake by me. Its just the height.kuruman said:And why do you think the CM is at height ##\frac{0.195}{2}~m## just before the carton tips over? That's its height when the carton sits flat on the conveyor belt.
I assume you mean Md2, not M+d2.javii said:I_p= 1/12M(l^2+a^2)+M+d^2
I_p=1/12M*l^2+1/12*a^2+M+d^2 ?
So what do you get now for the vertical displacement of the mass centre?javii said:I see, it is a mistake by me. Its just the height.
Thanks