Calculate Y-parameters of a capacitor in parallel

[Bromio]

Homework Statement

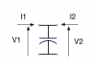
Calculate the Y parameters of a capacitor in parallel (see the attached figure).

Homework Equations

Y-Parameters:
I_1=Y_{11}V_1+Y_{12}V_2
I_2=Y_{21}V_1+Y_{22}V_2

Y_{11} = \frac{I_1}{V_1} when V_2=0
Y_{12} = \frac{I_1}{V_2} when V_1=0
Y_{21} = \frac{I_2}{V_1} when V_2=0
Y_{22} = \frac{I_2}{V_2} when V_1=0

The Attempt at a Solution

I've tried to use formulas written above, but when V_2=0, then V_1=0, so Y_{11}\to\infty?

The same happens when I try to find Y-parameters of a resistor in parallel.

Thank you.

 

[gneill]

Since there's only the one essential node in the circuit, V1 = V2 always. So finding the Y-Parameters by shorting a port and expecting the other port to have some voltage other than zero is, well, problematical!

You may have more luck with the Z-Parameters... then consider how the Y-matrix is related to Z-matrix. What conclusions can you draw?

 

[Bromio]

OK. Thanks.

So,
V_1 = Z_{11}I_1 + Z_{12}I_2
V_2 = Z_{21}I_1 + Z_{22}I_2

I have no problem finding Z_{11}:
Z_{11} = \left.\frac{V_1}{I_1}\right|_{I_2=0} = \frac{1}{j\omega C}

However, when finding Z_{12} I'm not sure if I draw the circuit properly in order to calculate the parameters. I mean I_1=0 and V_1=V_2, so Z_{12} = \left.\frac{V_1}{I_2}\right|_{I_1=0} = \left.\frac{V_2}{I_2}\right|_{I_1=0}= \frac{1}{j\omega C}.

If that's true, all Z-parameters are equal to Z_{11} = \frac{1}{j\omega C}.

Is this correct?

Thanks!

 

[gneill]

OK. Thanks.

So,
V_1 = Z_{11}I_1 + Z_{12}I_2
V_2 = Z_{21}I_1 + Z_{22}I_2

I have no problem finding Z_{11}:
Z_{11} = \left.\frac{V_1}{I_1}\right|_{I_2=0} = \frac{1}{j\omega C}

However, when finding Z_{12} I'm not sure if I draw the circuit properly in order to calculate the parameters. I mean I_1=0 and V_1=V_2, so Z_{12} = \left.\frac{V_1}{I_2}\right|_{I_1=0} = \left.\frac{V_2}{I_2}\right|_{I_1=0}= \frac{1}{j\omega C}.

If that's true, all Z-parameters are equal to Z_{11} = \frac{1}{j\omega C}.

Is this correct?

Yup.

 

[Bromio]

In that case I have the same problem as before.

I know that Y_{11}=\frac{Z_{22}}{\Delta_Z}, where \Delta_Z = Z_{11}Z_{22}-Z_{12}Z_{21}.

Because Z_{11} = Z_{12} = Z_{21} = Z_{22} = \frac{1}{j\omega C}, \Delta_Z = 0, so Y_{11}\to\infty.

Where's the mistake?

Thank you.

 

[gneill]

No mistake. Since the determinant of the impedance matrix is zero, there's no inverse, hence no finite Y-parameters.

If you consider the circuit, the two ports are directly wired together. Hence in reality it's a single port device.

 

[Bromio]

Thank you.

I really wanted to find the Y-parameter matrix of a Schottky diode working as mixer, whose model is this:

Should I conclude that it isn't posible to get it by adding capacitor Cj and resistor Rj Y-matrices, going to Z-parameters, adding the result with Rs Z-matrix, and finally going back to Y-parameters?

Thanks.

 

[rude man]

The Schottky is obviously part of a larger circuit - if you show us that then possibly we can advise you as to exploiting the conveniences of 2-terminal matrices, if any.