Ideal Transformer Homework Solution

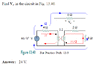
[p75213]

Homework Statement

See attached

Homework Equations

V2/V1=I1/I2=n n=2

The Attempt at a Solution

$$\begin{array}{l} {\rm{Mesh 1: }} & 4{I_1} + {V_1} = 60 \\ {\rm{Mesh 2:}} & 10{I_2} - {V_2} - 2{I_3} = 0 \\ {\rm{Mesh 3:}} & - 2{I_2} + 10{I_3} + {V_2} - {V_1} = 0 \\ {I_1} = - 2{I_2} & & {V_1} = \frac{{{V_2}}}{{ - 2}} \\ {\rm{Mesh 1: }} & - 8{I_2} - 0.5{V_2} + 0{I_3} = 60 \\ {\rm{Mesh 2:}} & 10{I_2} - {V_2} - 2{I_3} = 0 \\ {\rm{Mesh 3:}} & - 2{I_2} + 1.5{V_2} + 10{I_3} = 0 \\ \end{array}$$

When I put these equations into a maths program I get I3=7.5A which means that Vo=60V not 24V.

 

[gneill]

Transformers can cause some problems for standard mesh analysis; transformer coupling relates their primary and secondary loops more intimately than a simple component like a resistor shared by the loop would. The constraint implied by the transformer equation I₁ = -2I₂ is not just for the mesh currents, but the actual (total) currents that must flow through the transformer windings. That means that the actual current flowing through the 2Ω resistor also has this constraint. Your mesh current I₃ cannot be allowed to affect this total current flowing through this resistor!

If I may offer a suggestion: Assume that the current in the primary winding is i1 and the current flowing out of the dot on the secondary is i1/2. That means there is a mesh current of i1/2 flowing upwards through the 8Ω resistor in the second loop. Then write a KVL equation for the path around the outside of the circuit (let the current through the upper 8Ω resistor be i2). You should be able to solve for i2 rather handily...

 

[p75213]

Hi GNeill,
From your hints I went back to the equation V1I1=V2I2:

$$\begin{array}{l} {V_1}\left( {{I_1} - {I_3}} \right) = {V_2}\left( {{I_2} - {I_3}} \right) \\ \frac{{{V_2}}}{{{V_1}}} = \frac{{\left( {{I_1} - {I_3}} \right)}}{{\left( {{I_2} - {I_3}} \right)}} = - n \\ {I_1} = - n\left( {{I_2} - {I_3}} \right) + {I_3} \\ {I_1} = - 2\left( {{I_2} - {I_3}} \right) + {I_3} \\ {I_1} = 3{I_3} - 2{I_2} \\ {\rm{Mesh Equations:}} \\ - 8{I_2} - 0.5{V_2} + 12{I_3} = 60 \\ 10{I_2} - {V_2} - 2{I_3} = 0 \\ - 2{I_2} + 1.5{V_2} + 10{I_3} = 0 \\ \end{array}$$I3 is now 3A which makes the voltage 24V.