- #1
oreosama
- 51
- 0
Homework Statement
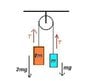
a load of bricks of mass m hangs from one end of a rope that passes over a small frictionless pulley. a counterweight, twice as heavy, is suspended from the other end of the rope. given m determine the accel of the masses and the tension in the rope
Homework Equations
f=ma
The Attempt at a Solution
Fa=-2mg + T
2m*a=-2mg + T
a= (-2mg+T)/2m
plug in accel in other force
Fb = -mg + T
m((-2mg+T)/2m) = -mg + T
-2mg + T = -2mg + 2T
T = 2T
T=0?
i have no idea if I am doing anything remotely close to the right path, if I'm way off please explain like a baby as I'm confused thanks for help