Calculating Acceleration of Blocks on a Ramp

[shell4987]

Homework Statement

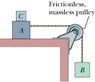
In Fig. 6-35, blocks A and B have weights of 51 N and 23 N, respectively. (a) Determine the minimum weight of block C to keep A from sliding if μs between A and the table is 0.23. (b) Block C suddenly is lifted off A. What is the acceleration of block A if μk between A and the table is 0.12?
**image is attached**

Homework Equations

fxnet= T-fs=ma
fymet= FN-Wc-Wa=0

fxnet=T-UkFn=ma

The Attempt at a Solution

I completed part (a) and got 4.8 to be the answer, however, I didnt get part (b), I tried to use the tension I got from part (a) and put it in the 3rd equation above and got -14,472 which is obviously not correct. Can anyone tell me what I'm doing wrong?

 

[Doc Al]

The tension is not the same once things start accelerating. You'll have to set up equations for both masses and solve for the acceleration (and new tension).

 

[shell4987]

Okay, I did that... the second two equations were Fxnet= T-Uk(WA)=ma and Fynet= Wb-T=ma and when I added them together I got Wb - Uk(Wa)=(ma + mb)a and then solved for a and got 0.23 for the answer, and it was yet again wrong. What am I doing that's not right again?

 

[Doc Al]

Be sure when calculating ma + mb that you are adding the masses and not the weights.