Juntao
- 45
- 0
Picture is attached.
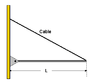
The above figure shows a uniform iron beam of mass 254 kg and length L = 3 m. The cable holding the beam in place can take a tension of 1300 N before it breaks. (You may ignore the small mass of the cable in this calculation.)
======
a)What minimum length of the cable?
b) Assume the cable is made of steel and has a diameter of 1". How much will it stretch before it breaks?
============
Okay. I am stuck on part a so far. I know that this is a static equilibrium, therefore, the summation of all the forces in x and y direction equal zero.
Also, the summation of torques must also equal zero.
But I'm not sure how to write out the equations. Can someone give me a lending hand?
The above figure shows a uniform iron beam of mass 254 kg and length L = 3 m. The cable holding the beam in place can take a tension of 1300 N before it breaks. (You may ignore the small mass of the cable in this calculation.)
======
a)What minimum length of the cable?
b) Assume the cable is made of steel and has a diameter of 1". How much will it stretch before it breaks?
============
Okay. I am stuck on part a so far. I know that this is a static equilibrium, therefore, the summation of all the forces in x and y direction equal zero.
Also, the summation of torques must also equal zero.
But I'm not sure how to write out the equations. Can someone give me a lending hand?