ddobre
- 33
- 2
Homework Statement
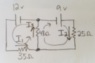
Calculate the magnitudes and directions of the currents in each of the 3 resistors in the circuit above, if...
(a) ...both batteries have zero internal resistance.
(b) ...each battery has an internal resistance of 1.0 Ω.
Homework Equations
I1 = I2 + I3 (Node Law)
The Attempt at a Solution
I tried to use the node law to define the direction of the current, and for part a) I got I3 = .1452A,
I1 = .06398A, and I2 = .08122A. I'm not sure if this is correct but this is how I tried to solve part a). For part b), since the batteries now have internal resistance, I added two 1 ohm resistors to the circuit, on the left and right of the node at the top, (next to the negative terminals of the batteries). But, I had issues trying to solve the series of equations with 5 resistors in the circuit. I tried to solve for each anyway, but with poor results, (I couldn't narrow down one current). I would try to solve with an Req, but I need the current through each resistor. Any advice?