psy
- 13
- 1
Hello! I have the following problem and attempt for solution.
Two equal, small conductive balls hang on two long non-conductive threads attached to a hook. The balls are charged with the same charges and are located 5 cm apart. One of the balls will now be decharged. What is the new distance between the balls?
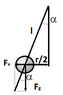
So the Force between the balls : F= k ⋅ q1 ⋅ q2 / r^2 .
Also there is the gravitational force F= m⋅g.
sinα = (r/2)/l ; tanα= Fe/Fg.
l- length of the thread
sinα = tanα ; (r/2)/l = Fe/Fg → Fe= r⋅m⋅g / 2⋅l . Putting this in the above equation :
Fe= k ⋅ q1 ⋅ q2 / r^2 → r^2 = k ⋅ q1 ⋅ q2 / Fe → r^2 = (k ⋅ q1 ⋅ q2) / (r⋅m⋅g / 2⋅l ).
Now if i don't have any given length of the thread and mass of the balls, how is it possible to calculate the distance?
Is there another way to calculate it?
Kind regards
Two equal, small conductive balls hang on two long non-conductive threads attached to a hook. The balls are charged with the same charges and are located 5 cm apart. One of the balls will now be decharged. What is the new distance between the balls?
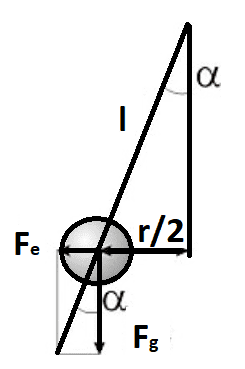
So the Force between the balls : F= k ⋅ q1 ⋅ q2 / r^2 .
Also there is the gravitational force F= m⋅g.
sinα = (r/2)/l ; tanα= Fe/Fg.
l- length of the thread
sinα = tanα ; (r/2)/l = Fe/Fg → Fe= r⋅m⋅g / 2⋅l . Putting this in the above equation :
Fe= k ⋅ q1 ⋅ q2 / r^2 → r^2 = k ⋅ q1 ⋅ q2 / Fe → r^2 = (k ⋅ q1 ⋅ q2) / (r⋅m⋅g / 2⋅l ).
Now if i don't have any given length of the thread and mass of the balls, how is it possible to calculate the distance?
Is there another way to calculate it?
Kind regards