stunner5000pt
- 1,443
- 4
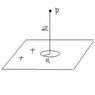
A large flat nonconducting surface carries a uniform surface charge density of sigma. A small circular hole of radius R has been cut out from this surface as in the figure. Ignore the fringing of the fierld lines around all the edges and calculate the electric field at point P located a distance z from the centre of the hole. (Hint says to refer to the electric field due to a charged disc and use superposition)
well I am using the hint and thinking that the field would the electric field due to a nonconducting surface less the electric field due to this charged disc.
so would it be E = \frac{\sigma}{2\epsilon_{0}} - \frac{\sigma}{2\epsilon_{0}} (1- \frac{z}{\sqrt{z^2+r^2}}) = \frac{\sigma z}{2 \epsilon_{0} \sqrt{z^2+R^2}}
is this correct? PLease do advise! Thank you!
well I am using the hint and thinking that the field would the electric field due to a nonconducting surface less the electric field due to this charged disc.
so would it be E = \frac{\sigma}{2\epsilon_{0}} - \frac{\sigma}{2\epsilon_{0}} (1- \frac{z}{\sqrt{z^2+r^2}}) = \frac{\sigma z}{2 \epsilon_{0} \sqrt{z^2+R^2}}
is this correct? PLease do advise! Thank you!