stunner5000pt
- 1,447
- 5
Seems quite strange that i can't solve simple questions like this... but on the other hand applying Gauss Law to cylinders spheres and such isn't that hard for me... ANYWAY
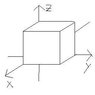
One of the cube's edges is placed at the origin.
A cube with edges 1.4m is oriented as shown in the diagram. Find the flux and the charge inside the cube when the electric field is
a) (3 Nm/c) y j
b) (-4N/C)i + [6N/C + (3Nm/C)y] j
for a) since there are TWO faces in the X only. THe Y and Z componenets are orthogonal to the field thus are zero. \Phi = 2 \int E \bullet dA = \frac{q_{enc}}{\epsilon_{0}}
\Phi = 2 \int 3y [d(y^2)] = 2 \int 6y^2 dy = 4y^3
since y = 1.4m flux is 10.976 Nm^2/C
the charge in teh cube as a result is 10.976=\frac{q_{enc}}{\epsilon_{0}}
for b), since there are two faces for the X and Y sides
in the case of the X the field is constnat so \int E dA = EA
\Phi = 12(1.4)^2 + 2 \int (6+3y)2y dy
blah blah blah leads to
\Phi = 12(1.4)^2 + 2 [6(1.4)^2 + 2(1.4)^3]
and plugging that equal to Qenc/epsilon yeilds the induced charge
Am i right? If i am wrong please do tell! Thank you so much!
One of the cube's edges is placed at the origin.
A cube with edges 1.4m is oriented as shown in the diagram. Find the flux and the charge inside the cube when the electric field is
a) (3 Nm/c) y j
b) (-4N/C)i + [6N/C + (3Nm/C)y] j
for a) since there are TWO faces in the X only. THe Y and Z componenets are orthogonal to the field thus are zero. \Phi = 2 \int E \bullet dA = \frac{q_{enc}}{\epsilon_{0}}
\Phi = 2 \int 3y [d(y^2)] = 2 \int 6y^2 dy = 4y^3
since y = 1.4m flux is 10.976 Nm^2/C
the charge in teh cube as a result is 10.976=\frac{q_{enc}}{\epsilon_{0}}
for b), since there are two faces for the X and Y sides
in the case of the X the field is constnat so \int E dA = EA
\Phi = 12(1.4)^2 + 2 \int (6+3y)2y dy
blah blah blah leads to
\Phi = 12(1.4)^2 + 2 [6(1.4)^2 + 2(1.4)^3]
and plugging that equal to Qenc/epsilon yeilds the induced charge
Am i right? If i am wrong please do tell! Thank you so much!
Attachments
Last edited: