Istiak
- 158
- 12
- Homework Statement
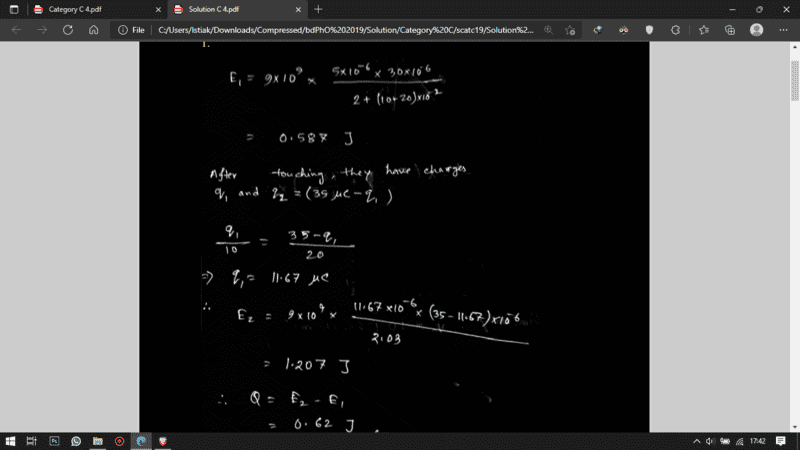
- Two solid conducting sphere of radius ##10 cm## and ##20 cm## having ##5\mu C## and ##30\mu C## charges respectively are kept at 2 meter distance. Then, they are connected by a conducting wire. Find the amount of heat generated in this process.
- Relevant Equations
- ##U=\frac{1}{4\pi\epsilon_0} \frac{q_1 q_2}{r}##
Generally, energy is ##U=9\times 10^{9} \times \frac{5\times 10^{-6}30\times 10^{-6}}{2+(10+20)\times 10^{-2}}=0.5869 J##
<br/>
After touching, they have charges
##q_1 and q_2 = 35\mu C-q_1##
##\frac{q_1}{10}=\frac{35\mu C-q_1}{20}##
I was wondering where 1/10 and 1/20 coefficients come from. I was thinking to convert q_2 to q_1 but end up with nothing.
<br/>
After touching, they have charges
##q_1 and q_2 = 35\mu C-q_1##
##\frac{q_1}{10}=\frac{35\mu C-q_1}{20}##
I was wondering where 1/10 and 1/20 coefficients come from. I was thinking to convert q_2 to q_1 but end up with nothing.
Last edited: