Calculating equilibrant in regular hexagon

[sareba]

Homework Statement

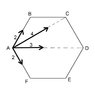
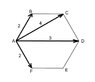
In a regular hexagon, ABCDEF, forces of magnitude 2N, 4N, 3N and 2N act along the lines AB, AC, AD and AF respectively. Find the equilbrant of the given forces and verify that is equal and opposite to their resultant.

The Attempt at a Solution

I realized that AB + BC is equal to AC, which is 4N, so BC should be 2N and AC + CD is equal to AD, which is equal to 3N, so CD should be equal to -1N? but also since AC is parallel to and twice as much as BC it should be 4N but it is 3N so which of my assumption is wrong? Also resolving didnt get me the right answer maybe i didnt do it right.

The answer is 8.7 N at 46.7° to BA.
P.S I am new to this forum so go easy if i didnt post it right or anything. :D

 

[CWatters]

I realized that AB + BC is equal to AC, which is 4N, so BC should be 2N

No. AB and BC are at different angles so it's not simply a matter of AB + BC = AC. The only way 2 + 2 = 4 in vector addition is if the two vectors are parallel and they aren't.

I make the drawing something like this..

 

[tiny-tim]

hi sareba!

I realized that AB + BC is equal to AC, which is 4N, so BC should be 2N and AC + CD is equal to AD, which is equal to 3N, so CD should be equal to -1N? but also since AC is parallel to and twice as much as BC it should be 4N but it is 3N so which of my assumption is wrong? Also resolving didnt get me the right answer maybe i didnt do it right.

to be honest, i don't understand any of this …

you seem to picturing it the wrong way ​

look at CWatters' excellent diagram, and start again

(you'll probably have to add the components, using sin and cos )

 

[CWatters]

I think I see his problem. If you mistakenly draw the vector acting in the direction AB the full length of the side AB (and others likewise) then easy to confuse the hexagon with a vector head-to-tail diagram.

For example this diagram is totally incorrect but it might fool you into thinking that AB+BC=AC. However it's not to scale. If the sides were 2 units long then AC would not be 4 units long nor would AD be 3 units long.

 

[sareba]

Oh... I understand now! *facepalm* I must be so dumb. Anyway thanks a lot guys! Really impressed.