Calculating Force F Required for Frictionless Blocks to Remain at Rest

AI Thread Summary
To determine the force F required to keep blocks M1 and M2 at rest relative to block M, the acceleration due to M2's weight must be countered. Since there is no friction, the force F must provide enough horizontal push to prevent M2 from falling. The condition for M1 to remain stationary with respect to M is that M1 must not move, which means M2 must also remain in place. Therefore, the applied force F must balance the gravitational force acting on M2. Understanding these dynamics is crucial for solving the problem accurately.
annatar
Messages
24
Reaction score
0

Homework Statement



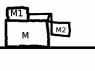
What is the magnitude of force F (which is pushing from the left on M) required to keep M1 and M2 relatively at rest to M?

Ignore all friction.

See attached diagram


Homework Equations



Newton's laws

The Attempt at a Solution



Well...If M is at rest, M1 and M2 will have an acceleration due to M2's weight.
When force F appears though, M2 will be pushed horizontally by M since they are in contact.

That's all I know atm.
 

Attachments

  • M.png
    M.png
    3.3 KB · Views: 377
Physics news on Phys.org
The question asks about a force on M that allows "M1 and M2 to remain relatively at rest to M".

So what is the condition between M1 and M, such that M1 stays at rest with respect to M? If M1 does not move with respect to M, the M2 doesn't fall.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Find the acceleration of the system (2 blocks sliding on a table)
Replies
23
Views
2K
How much force does the 20 kg block exert on the 10 kg block?
Replies
17
Views
2K
Calculating Net Force of 3 Blocks in an Elevator
Replies
9
Views
2K
Newton's law problem: Pushing 2 stacked blocks on a horizontal table
Replies
13
Views
3K
Newton's laws — Two stacked blocks sliding on a frictionless floor
Replies
17
Views
3K
When Friction the block m2 start to move?
Replies
11
Views
2K
Kleppner - blocks and a compressed spring
Replies
3
Views
3K
Distribution of Energy when work is done on a system of 2 masses connected by a spring
Replies
17
Views
1K
How Does a Force Affect Spring Length Between Two Equal Mass Blocks?
Replies
2
Views
2K
Friction/spring/inclined plane problem
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top