Calculating gain of a phase detector

[ollie456]

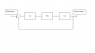
I have a linear model of a phase detector (phase lock loop) represented by the block diagram below. It is designed to maintain zero difference in phase between the input carrier signal and a local voltage controlled oscillator.

Phase demand→Ka→F(s)→K/s→Phase output

F(s) = 10(s+10)/(s+1)(s+100)

We want to minimise the steady state error for a ramp change in the phase information signal.

Can anyone help determine the limiting value of the gain KaK = Kv in order to maintain a stable system.

 

[milesyoung]

We usually work with the open-loop function of the system when determining its margins for closed-loop stability. I assume you're showing the closed-loop function since there's no feedback loop included. Maybe you could show a block diagram of your system before any reductions are made and we can go from there?

The system you have shown has infinite gain margin, be it in open or closed loop.

 

[ollie456]

I've attached a more accurate block diagram which has the feedback look included.

 

[milesyoung]

Right, are you familiar with root-locus and/or frequency-response analysis?

 

[ollie456]

I have been trying to use the root locus approach, I'm not sure about frequency response. I worked the closed loop transfer function to 100K²/(s+1)(s+100)+K and then used the quadratic formula to try and obtain roots getting -50.5≠.5√9801-4k. The steady state error acceptable is 1° for a ramp signal of 100rad/s. I am confused at how to go about calculating gain for a ramp change compared with a step change.

 

[milesyoung]

First thing, I think you took a wrong turn somewhere in calculating the closed-loop transfer function. You could show the details of your work if you want some pointers, but you're going to end up having to find the roots of a cubic polynomial. That's not an intractable problem per se, but root-locus analysis is, in large part, about finding the locus of the roots of the characteristic polynomial without having to actually solve it analytically (which can be hard to impossible).

It's difficult to see on this plot since I have no idea how to set the gain and axis limits manually, but hopefully it will give you the basic idea. The locus never enters the right-half plane, i.e. your system is stable for any gain.

I am confused at how to go about calculating gain for a ramp change compared with a step change.

It's not much different. Your system is type 1 since you have a free integrator so it will have a bounded [strike]output[/strike] error for a ramp input. Do you know what the error constant is for a ramp input?

 

[ollie456]

I know the error constant is the velocity error constant Kv, i now have the transfer function as k/(100s)(s+1)(s+100)

 

[milesyoung]

I know the error constant is the velocity error constant Kv ...

Great You need to use the velocity error constant instead of the position error constant when your input is a ramp signal but otherwise the procedure is the same. Show your work and where you get stuck.

... i now have the transfer function as k/(100s)(s+1)(s+100)

That's still not correct. Reminder:

The open-loop function L(s) is given by:
L(s) = Ka*K*F(s)/s

The closed-loop function T(s) is given by:
T(s) = L(s)/(1 + L(s))

It would help a great deal if you could show each step of what you did in order to arrive at your result.

 

[ollie456]

Ive attached some workings of the open loop transfer function calculation, is this evaluated at s=0 to obtain Kv

 

[milesyoung]

Ok so, third line, there's a problem with what you're doing in the denominator:
$$\frac{1}{10}(s + 1)(s + 100) \neq \left(\frac{s + 1}{10}\right) \left(\frac{s + 100}{10}\right)$$

You should be able to tell from:
$$\left(\frac{s + 1}{10}\right) \left(\frac{s + 100}{10}\right) = \frac{1}{10}(s + 1)\left(\frac{s + 100}{10}\right) = \frac{1}{10}\frac{1}{10}(s + 1)(s + 100) = \frac{1}{100}(s + 1)(s + 100)$$

Also:
$$K_v = \lim_{s \rightarrow 0}sL(s)$$

 

[ollie456]

Thanks, I've attached my working to get a value of 0.1 for Kv is this correct?

 

[milesyoung]

The L(s) you started out with in your first attachment was correct. You've changed it around some in your second one.

So you have:
$$L(s) = K_a K \frac{10(s + 10)}{s(s+1)(s+100)} \\ K_v = \lim_{s \rightarrow 0}s L(s) = \lim_{s \rightarrow 0}s K_a K \frac{10 (s + 10)}{s(s+1)(s+100)} = \lim_{s \rightarrow 0}K_a K \frac{10 (s + 10)}{(s+1)(s+100)} = K_a K \frac{10 \cdot 10}{1 \cdot 100} = K_a K$$
The steady-state error for your system is then given by:
$$e_{ss} = \frac{\alpha}{K_v} = \frac{\alpha}{K_a K}$$
where $\alpha$ is the slope of your ramp signal.

Now you just need to come up with a value for your gain $K_a K$ such that your constraint on the steady-state error is satisfied.

 

[ollie456]

So this is the value of the gain Kv that satisfies a steady state error of 1° with a ramp signal (slope) of 100 rads? Is there a limiting value of gain Kv to keep the system stable, or is this it?

 

[milesyoung]

So this is the value of the gain Kv that satisfies a steady state error of 1° with a ramp signal (slope) of 100 rads?

Yes Usually you write it as an upper bound on the steady-state error, which gives a lower bound on the gain:
$$e_{ss} = \frac{\alpha}{K_a K} \leq 1\frac{\pi}{180} \Leftrightarrow K_a K \geq \frac{180\alpha}{\pi}$$

Is there a limiting value of gain Kv to keep the system stable, or is this it?

As we talked about before, your system is stable for any gain.

 

[ollie456]

How would you go about determining the location of the poles for the system?

 

[milesyoung]

How would you go about determining the location of the poles for the system?

I would use a numerical algorithm to find the roots of the characteristic polynomial of the closed-loop system:
http://en.wikipedia.org/wiki/Root-finding_algorithm

Which is basically what your computer does with varying loop gain when you ask it to plot the root locus for the system.

The open-loop function usually tells you all you need to know about the performance of the closed-loop system. If its characteristic polynomial admits an analytical solution, it rarely contributes significantly to your body of knowledge of the system.

It just occurred to me that this might just be a homework problem. Just FYI, if that's the case, there's a whole other forum for it on PF, which you should have used instead.