Wiz
- 21
- 0
Hi,
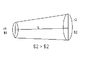
I have to find the rate of heat flow through a cross-section of the rod in steady state as shown in the figure.Thermal conductivity of the rod is K.
I have used a $(dollar) sign for theta.
The formula i know is ΔQ/Δt = [KA($2 - $1)] /x
where ΔQ/Δt is the heat current,where A is area of cross section and x is the thickness.
since the area of cross section varies.i think integration will be used...
can ANYBODY GUIDE ME THROUGH..??
[NOTE - THE FIGURE READ THAT $2 > $2 , which is a mistake and the correction is $2 > $1.]
Thanks,
I have to find the rate of heat flow through a cross-section of the rod in steady state as shown in the figure.Thermal conductivity of the rod is K.
I have used a $(dollar) sign for theta.
The formula i know is ΔQ/Δt = [KA($2 - $1)] /x
where ΔQ/Δt is the heat current,where A is area of cross section and x is the thickness.
since the area of cross section varies.i think integration will be used...
can ANYBODY GUIDE ME THROUGH..??
[NOTE - THE FIGURE READ THAT $2 > $2 , which is a mistake and the correction is $2 > $1.]
Thanks,