Little Dump
- 19
- 0
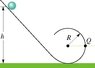
Ok there's this ball rolling down a ramp. The ball has some radius r and some mass m. At the bottom of the ramp there is a loop. The loop has radius R.
The question is, if the ball is 1/4 of the way completed the loop, what is the horizontal component of the net force on the ball. And it is also given that the ball starts up the ramp at height 6R.
Ok so I've been messing around, and what getting me is that when the ball starts the go up in the loop, gravity will do some work. The problem is, I do not know how to calculate the work done by gravity.
Perhaps I am doing the question wrong because I am analysing the rotation of the ball in the loop, not the actual rotation of the ball itself.
Basically what I am doing is using energy and here's my equations
mg(6R) + Wgrav = 1/2mv^2 + 1/2I(omega)^2 + mgR
and
v = R(omega)
so we make the substitution and solve for omega
then we go back and solve for v
the we do
a = v^2/R
and finally
F=ma
but I may be doing this completely wrong so any help will be great. Here is the original question with diagram:
A small solid marble of mass 12 g and radius 3.8 cm will roll without slipping along the loop-the-loop track shown in Fig. 12-33 if it is released from rest somewhere on the straight section of track. (a) From what initial height h above the bottom of the track must the marble be released if it is to be on the verge of leaving the track at the top of the loop? (The radius of the loop-the-loop is 4.0 m; Note that it is much greater than the radius of the marble.) (b) If the marble is released from height 6R above the bottom of the track, what is the horizontal component of the force acting on it at point Q?
The answer with these number is 0.840N.
The question is, if the ball is 1/4 of the way completed the loop, what is the horizontal component of the net force on the ball. And it is also given that the ball starts up the ramp at height 6R.
Ok so I've been messing around, and what getting me is that when the ball starts the go up in the loop, gravity will do some work. The problem is, I do not know how to calculate the work done by gravity.
Perhaps I am doing the question wrong because I am analysing the rotation of the ball in the loop, not the actual rotation of the ball itself.
Basically what I am doing is using energy and here's my equations
mg(6R) + Wgrav = 1/2mv^2 + 1/2I(omega)^2 + mgR
and
v = R(omega)
so we make the substitution and solve for omega
then we go back and solve for v
the we do
a = v^2/R
and finally
F=ma
but I may be doing this completely wrong so any help will be great. Here is the original question with diagram:
A small solid marble of mass 12 g and radius 3.8 cm will roll without slipping along the loop-the-loop track shown in Fig. 12-33 if it is released from rest somewhere on the straight section of track. (a) From what initial height h above the bottom of the track must the marble be released if it is to be on the verge of leaving the track at the top of the loop? (The radius of the loop-the-loop is 4.0 m; Note that it is much greater than the radius of the marble.) (b) If the marble is released from height 6R above the bottom of the track, what is the horizontal component of the force acting on it at point Q?
The answer with these number is 0.840N.