portuguese
- 15
- 0
Consider that the curve C (IR3) is the intersection between x2+2z2=2 and y=1.
Calculate the line integral:
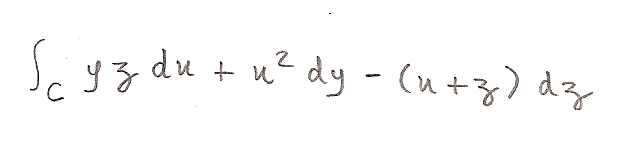 Note: The curve C is traversed one time in the counter-clockwise direction (seen from the origin of IR3).
Note: The curve C is traversed one time in the counter-clockwise direction (seen from the origin of IR3).
My attempt:
http://i.imgur.com/5EsJO.png
Can someone check? Thanks! :)
Calculate the line integral:
My attempt:
http://i.imgur.com/5EsJO.png
Can someone check? Thanks! :)
Last edited by a moderator:
 .
.