Calculating Line Integrals: Solving for Limits and Using Parametric Equations

Nachore · 2008-11-30T20:52:01+00:00

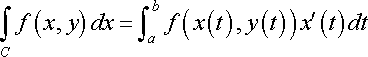
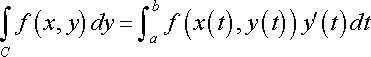
Evaluate the line integral \int y^(2) dx + xy dy from A(1,0) to B(-1,4) with C: x = 1-t, y = t^(2), 0≤t≤2 I used: Do I make the limits from 0 to 2? What do I do with the A(1,0) and B(-1,4)? Please help? Thanks.

Thread 'Finding the nth roots of a complex number'

There are two things I don't understand about this problem. First, when finding the nth root of a number, there should in theory be n solutions. However, the formula produces n+1 roots. Here is how. The first root is simply ##\left(r\right)^{\left(\frac{1}{n}\right)}##. Then you multiply this first root by n additional expressions given by the formula, as you go through k=0,1,...n-1. So you end up with n+1 roots, which cannot be correct. Let me illustrate what I mean. For this...

View full post »

Thread 'Solve this problem that involves induction'

Hello, This is the attachment, the steps to solution are pretty clear. I guess there is a mistake on the highlighted part that prompts this thread. Ought to be ##3^{n+1} (n+2)-6## and not ##3^n(n+2)-6##. Unless i missed something, on another note, i find the first method (induction) better than second one (method of differences).

View full post »

Thread 'Finding the nth roots of a complex number'

Thread 'Solve this problem that involves induction'

Similar threads

Hot Threads

Prove that the integral is equal to ##\pi^2/8##

Solving the wave equation with piecewise initial conditions

Area of loop in x-y plane

Calculating radius of gyration of plane figure about x-axis

Solve this problem that involves induction

Recent Insights

Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect

Insights What Exactly is Dirac’s Delta Function? - Insight

Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight

Insights Fixing Things Which Can Go Wrong With Complex Numbers

Insights Fermat's Last Theorem

Insights Why Vector Spaces Explain The World: A Historical Perspective