Calculating Line Integrals: Solving for Limits and Using Parametric Equations

Nachore · 2008-11-30T20:52:01+00:00

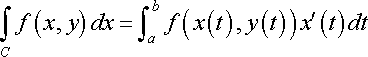
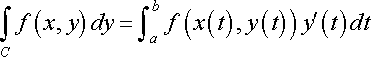
Evaluate the line integral \int y^(2) dx + xy dy from A(1,0) to B(-1,4) with C: x = 1-t, y = t^(2), 0≤t≤2 I used: Do I make the limits from 0 to 2? What do I do with the A(1,0) and B(-1,4)? Please help? Thanks.

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...

View full post »

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Similar threads

Hot Threads

Prove that the integral is equal to ##\pi^2/8##

Calculating radius of gyration of plane figure about x-axis

Solve this problem that involves induction

The volume of a "spherical cap" using triple integrals

Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##

Recent Insights

Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality

Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect

Insights What Exactly is Dirac’s Delta Function? - Insight

Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight

Insights Fixing Things Which Can Go Wrong With Complex Numbers

Insights Fermat's Last Theorem