rr263
- 8
- 0
Homework Statement
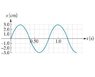
A 2.55 kg ball is attached to an unknown spring and allowed to oscillate. The figure shows a graph of the ball’s position x as a function of time . (A)What is the maximum kinetic energy of the vibrating ball? give answer in joules (B)When does it occur? (give answer in cm)
Homework Equations
I have attached a picture of the graph provided on the mastering physics site.
Kmax= (1/2)mv_i_^2
The Attempt at a Solution
Obviously, the mass is provided, but I am not sure how to find the velocity using the graph provided. Or do I simply use an initial velocity of zero? I didn't think using zero velocity was right, however, due to the fact that kinetic energy is only present at the central point in the graph.
Once again, my professor has disabled the "hints" option. Any help offered is appreciated! Thanks in advance!