rockchalk1312
- 38
- 0
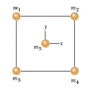
In the figure, a square of edge length 16.0 cm is formed by four spheres of masses m1 = 4.50 g, m2 = 2.80 g, m3 = 0.800 g, and m4 = 4.50 g. In unit-vector notation, what is the net gravitational force from them on a central sphere with mass m5 = 2.10 g?
F = G (m1m2/r2)
To get the radius as a diagonal I used pythagorean's theorem to calculate √162+162=11.31m.
I've solved that the force on m1 due to the center particle is (6.67E-11)(4.50 x 2.10/11.312) = 4.93E-12.
Solving the same way as above:
force on m2: 3.06E-12
force on m3: 8.76E-13
force on m4: 4.93E-12 (same mass as m1)
Was that the right radius to use in the law of universal gravitational equation?
Now that I have those I don't know how to break them into unit vector notation and find the net force? Help please? Figure attached.
F = G (m1m2/r2)
To get the radius as a diagonal I used pythagorean's theorem to calculate √162+162=11.31m.
I've solved that the force on m1 due to the center particle is (6.67E-11)(4.50 x 2.10/11.312) = 4.93E-12.
Solving the same way as above:
force on m2: 3.06E-12
force on m3: 8.76E-13
force on m4: 4.93E-12 (same mass as m1)
Was that the right radius to use in the law of universal gravitational equation?
Now that I have those I don't know how to break them into unit vector notation and find the net force? Help please? Figure attached.