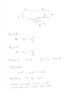Calculating Pressure Drop and Hole Size in a Pipe

[ramisaeed]

Hello everyone,

I got a question that has been bugging me for quite a while and i can't seem to find the answer for it, and here it is...

If we have a pipe let's say 20" in diameter, with a flow rate of 1 m^3/sec at a pressure of 10 psi, and we get a pressure drop of 9 psi, is it possible to know the size of the hole in the pipe that is causing this pressure drop? and what is the volume of water that is being lost from said hole?

Thanks for the help...

 

[gsal]

I lost you...where is the hole again? along the stream and part of the flow? on the side of the pipe?

 

[ramisaeed]

Along side the pipe (let's say a pipeline rupture)... I would like to know if there is a way to determine the size of that hole that would cause a reduction of 1 psi in pressure, and what is the rate of water that would come out from that hole...

yeah, sorry for not being clear in the first place, and if I am still not let me know...

Thanks

 

[mikeph]

I believe you can only determine the amount of water leaked, not the size of the hole. There are one too many degrees of freedom, because a smaller hole could leak the same amount of water if it emerged at a higher speed.

Try using Bernoulli's principle across a section of leaking pipe, the pressure difference will give you the velocity difference which, assuming the pipe is a constant cross section, give you the volume lost, but nothing more.

 

[gsal]

i think is do-able, but there is no unique solution...you may have to assume something and determine the rest...

for example, let's say that you have a run of 10 feet of that pipe and you know that there is a pressure loss of 10 psi...then you know you have a loss of 1psi per feet...

if you now have only a 9 psi loss ...you could start by assuming that you have a leak right in the middle of the run and then firgure out how much water leakage you need...knowing that the pressure loss up to the leak (half way) you already had 5 psi loss, etc...see what I am going?

 

[ramisaeed]

Hmm, sorry but i don't quite get it...

Assuming that the pipe from beginning to end has a constant 10 psi, and a drop to 9 psi signify a leak some where.

If there is a pressure drop that means the leak is causing the water to go out of the pipe, can we determine the amount that is being lost due to the pressure drop? not to mention the size of the hole that is needed to cause the loss of 1 psi from 10 to 9...

just bare with me, thanks...

 

[mikeph]

I've answered both these question. You can measure the amount that is lost but not the size of the hole.

 

[Studiot]

Here are some calculations, showing what is required to determine hole size (d₃)

Treating the problem as the pressure drop across a y junction with the hole as one leg discharging to atmosphere and ignoring friction. If significant lengths of pipe are involved then then the pipe friction coefficient and lengths need also be known.

 

[ramisaeed]

Thank you MikeyW & Studiot, i guess things are a bit clearer than where i was in the beginning...

 

[ramisaeed]

Okay, so i followed the equations that you proved me (Thanks for that),however there are somethings that just doesn't sit right with me, and as you can see here it is...

The flow rate for the pressure 2 is much higher than that of pressure 2

And diameter 3 is quite large for it to cause a drop of 1 bar...


Thanks for the comments & help thus far...

 

[Studiot]

Perhaps you should check your spreadsheet setup?
Remember head is measured in metres, feet or whatever.

Here is a realistic sample calculation an engineer looking for a hole in 300 feet of six inch supply pipe out in the Rockies might make. He wouldn't need a spreadsheet and could even do without a calculator (though they make it a bit easier).

Of course the water speed out of the (small) hole will be much faster than the main flow speed.

If you adjust your spreadsheet to follow this through you might be able to do what if simulations when you don't know the overall flow rate.

go well

 

[ramisaeed]

Thanks, can't believe i over looked the fact that the pressure was in units not relevant to the rest...

BTW, how did you calculate the head?

 

[ramisaeed]

YAY!, it worked, Thanks a lot for all your help, and sorry for the trouble...

 

[Studiot]

The hydraulic head is used by -yes - hydraulic engineers - and is simply the height above some datum level. Since this is a water engineering question I thought it appropriate.

In this case I have taken atmospheric pressure as datum. Atmospheric pressure = 32 feet.

go well