Calculating Resultant Force and Acceleration in a Simple Vector Problem

In summary, the child with a weight of 450 N is subject to a force P at an angle of 35° to the upward vertical while on a fairground ride. The resultant of P and the child's weight acts horizontally and has a magnitude of 315 N. The child's acceleration is directed horizontally to the left and has a magnitude of 7.00 m/s^2, according to the textbook. However, the book uses a value of 9.8 m/s^2 for gravity while you may have used 10 m/s^2, resulting in a slight difference in the calculated acceleration.
  • #1
furor celtica
69
0

Homework Statement



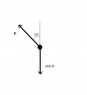
A child has weight 450 N. Whilst on a fairground ride the child is subject to a force P acting at 35° to the upward vertical, as shown in the diagram. Given that the resultant of P and the child’s weight acts horizontally,
a. Find the magnitude of the resultant
b. State the direction of the child’s acceleration
c. Find the magnitude of the child’s acceleration


Homework Equations





The Attempt at a Solution


My answers were the following
a. 315 N (to 3 s.f.)
b. The child’s acceleration is directed horizontally to the left
c. 7.00 m(s^2) (to 3 s.f.)

According to the textbook, my first two answers are correct, but the third is given as 6.86 m(s^2).
How is this possible? a = F/m = 315 / 45 = 7 m(s^2). Did I miss something?
 
Physics news on Phys.org
  • #2
forgot the diagram
 

Attachments

  • Untitled.png
    Untitled.png
    1.2 KB · Views: 471
  • #3
The book is using 9.8 m/s^2 for g, whereas you (apparently) used 10 m/s^2.
 

FAQ: Calculating Resultant Force and Acceleration in a Simple Vector Problem

What is a simple force vector problem?

A simple force vector problem involves calculating the magnitude and direction of a force acting on an object in a given situation. It can be solved using basic principles of physics, such as Newton's laws of motion.

How do I solve a simple force vector problem?

To solve a simple force vector problem, you first need to identify all the forces acting on the object and their directions. Then, you can use vector addition and trigonometry to determine the net force and its direction on the object.

What units are used to measure force in a simple force vector problem?

Force is typically measured in units of Newtons (N) in a simple force vector problem. Other common units include pounds (lb) and kilograms (kg).

Can a simple force vector problem have more than two forces acting on an object?

Yes, a simple force vector problem can have any number of forces acting on an object. However, it is important to remember that the net force is the vector sum of all the individual forces.

Are there any common mistakes when solving a simple force vector problem?

Yes, some common mistakes when solving a simple force vector problem include forgetting to include all the forces acting on an object, using the wrong trigonometric functions, and not paying attention to the direction of the forces.

Similar threads

Change in momentum: Child jumping from a swing on a playground
Replies
6
Views
1K
Find the magnitude of the child's acceleration
Replies
6
Views
440
Vector problem, magnitude of the force
Replies
30
Views
2K
How Does Nick's Acceleration Change When His Friend Pulls the Rope?
Replies
6
Views
3K
Vectors Directions: Where is this Resultant Vector Pointing?
Replies
14
Views
804
How Is the Force on a Child in a Roller Coaster Calculated?
Replies
3
Views
6K
What Are the Horizontal Forces Acting on a Child Pulling a Wagon?
Replies
3
Views
4K
Equilibrium of Forces and Torques on Sawhorses Supporting a Person on a Board
Replies
6
Views
1K
Calculation of Box's Acceleration on a Trailer with Friction
Replies
9
Views
1K
How to calculate the force exerted by the "tendon" on the "tibia" bone?
Replies
4
Views
557

Hot Threads

Recent Insights

Back
Top