Calculating Second Moment of Aria for Hollow Square Beams

  • Thread starter Thread starter a5hl3yi
  • Start date Start date
  • Tags Tags
    Moment
AI Thread Summary
To calculate the second moment of area for a hollow square beam, first determine the second moment of area for the outer solid square and then subtract the second moment of area for the inner square. The formula involves calculating the area moment for both the outer square (100mm x 100mm) and the inner square (70mm x 70mm). The correct approach is to compute the moment of area for the outer square and then subtract the moment of area for the inner square. This method provides the accurate second moment of area for the hollow square beam.
a5hl3yi
Messages
12
Reaction score
0
Question:

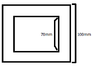
How do you work out the second moment of aria for a hollow square beam?

Attempt:

I have looked over my notes and it says how to get the second moment of aria for all beams but a hollow square one. It has I beam, Circulare beams, Rectangular...

How do you go about working it out for a hollow square beam?
 

Attachments

  • shtsrhrs.png
    shtsrhrs.png
    589 bytes · Views: 480
Physics news on Phys.org
Basically you just take the area moment of a solid square 100mm a side and subtract off the inside.
 
thanx.

So does that mean I would work out (100mm x 100mm) - (70mm x 70mm) and us that as the aria in the formula or work out the Moment of aria for the 100mm x 100mm and take off the moment of aria for a 70mmx70mm square?
 
Last edited:

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

How to take a moment into account for deflection of a beam
Replies
8
Views
2K
Calculating Moment of Inertia for Hollow Cylinder w/ Water
Replies
40
Views
5K
Moment of Inertia with pulley and two masses on a string (iWTSE.org)
Replies
8
Views
12K
How Long for a Beam of Light to Reach Earth?
Replies
21
Views
1K
Equivalent system (force+couple moment) of a loaded beam
Replies
9
Views
2K
Understanding The Concept Of Moments
Replies
6
Views
2K
Tension in two ropes attached to a beam
Replies
8
Views
10K
Velocity of a hollow cylinder at the bottom of an incline
Replies
9
Views
4K
Transfer of forces from a pulley to a beam
Replies
8
Views
5K
Solving a Homework Problem with One Pivot
Replies
10
Views
2K

Hot Threads

Recent Insights

Back
Top