Calculating Tension & Force of Steel Beam & Load

[Raid]

The problem is:
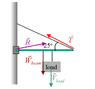
A uniform steel beam of length 4.50 m has a weight of 4500 N. One end of the beam is bolted to a vertical wall. The beam is held in a horizontal position by a cable attached between the other end of the beam and a point on the wall. The cable makes an angle of 25.0° above the horizontal. A load whose weight is 12000 N is hung from the beam at a point that is 3.30 m from the wall.

(a) Find the magnitude of the tension in the supporting cable.
(b) Find the magnitude of the force exerted on the end of the beam by the bolt that attaches the beam to the wall.

My thoughts on (a):
The torque caused by the beam itself = (2.25m*4500N)
The torque caused by the load = (3.3m*12000N)
Therefore the vertical component of the cable's tension is equal to the
sum of the two torques (49725 t)
To get the tension, I tried 49725 t/sin25 and this does not work

Any help would be greatly appreciated!

 

[Pyrrhus]

you forgot the lever arm of the vertical component of the tension.

 

[Raid]

I'm sorry, but what what do you mean by "the lever arm of the vertical component"?

 

[Pyrrhus]

i mean sum torques about the bolt on the vertical wall.

-(4500)(2.5) - (12000) (3.3) + T \sin 25^{o} (4.5) = 0

4.5 is the lever arm i meant.

 

[Raid]

Thank you so much!