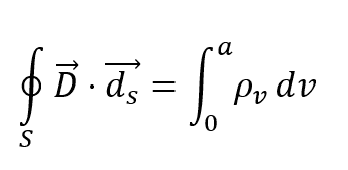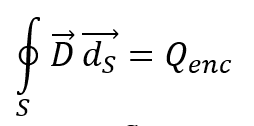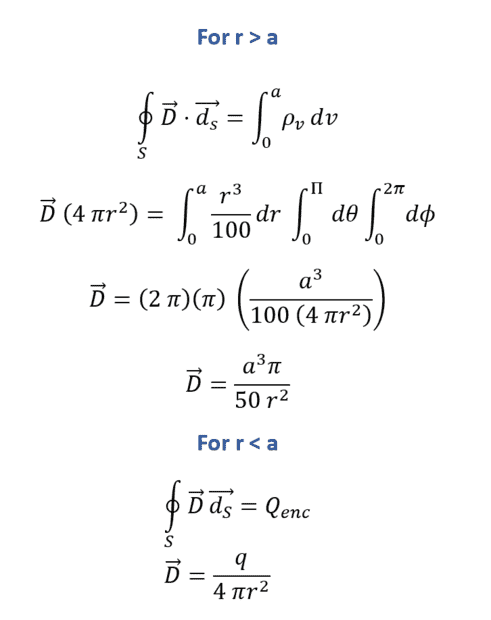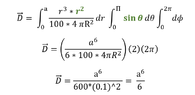SUMMARY
The discussion centers on calculating the charge when the electric field density is zero, specifically addressing the integration of charge density over a spherical volume. Participants clarify that the variable 'r' represents the integration variable, while 'R' is a constant distance for evaluating the field. The correct integral for charge density involves using the limits from 0 to 'a' and should yield a charge of -2.09e-8 C, confirming that the point charge at the center behaves like a point charge of zero from outside the sphere.
PREREQUISITES
- Understanding of electric field concepts and charge density
- Familiarity with spherical coordinates and integration techniques
- Knowledge of the relationship between charge density and total charge
- Proficiency in handling mathematical notation and variables in physics
NEXT STEPS
- Study the derivation of electric field equations for spherical charge distributions
- Learn about the application of Gauss's Law in electrostatics
- Explore advanced integration techniques in multiple dimensions
- Review common mistakes in variable notation and dimensional analysis in physics
USEFUL FOR
Physics students, electrical engineers, and anyone involved in electrostatics or charge distribution calculations will benefit from this discussion.