freddy13
- 12
- 0
Homework Statement
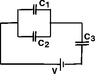
Three capacitors having capacitance C1 = 3.00 microF, C2 = 8.50 microF and C3 = 15.0 microF are connected to a 24.0 V battery as shown. Calculate the charge on C3.
Homework Equations
$$ C_{eq}= \left ( \frac{1}{C_1+C_2} + \frac{1}{C_3}\right )^{-1}$$
Q = CΔV
The Attempt at a Solution
First I attempted to find the Capacitance saying that C1+C2= 11.5μC through the parallel addition of capacitors. From here, I plugged everything into the
Ceq=((1/C1+C2(1/C3))-1
equation and got my capacitance which was 2.74 μF. I took the result and plugged all of my values into the Q = CΔV equation, and got a final value of 57.096 μC, or 5.71*10-5 C.
I tried another way and got the same answer, so, any suggestions would be great. I think I messed up somewhere with the units.
Attachments
Last edited: