You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculating the Length of a Segment Joining Centers of Inscribed Circles
- Thread starter Chikawakajones
- Start date
AI Thread Summary
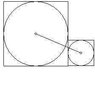
The discussion centers on calculating the length of the segment connecting the centers of inscribed circles in two adjacent squares with areas of 4 cm² and 196 cm². Participants debate the correct method, with one suggesting the use of a right-angled triangle to find the hypotenuse, while another argues for a simpler approach based on the properties of inscribed circles. The correct calculation involves determining the radii of the circles, which are half the side lengths of the squares, leading to a final answer of 10. Disagreements arise over the accuracy of proposed methods and answers, with one participant mistakenly using incorrect values for the radii. Ultimately, the consensus leans towards the right method being crucial for solving the problem accurately.
Physics news on Phys.org
theriddler876
- 98
- 0
it's the square root of four plus the square root of 196 and all that over two
Chikawakajones
- 22
- 0
does anyone agree/disagree?
daster
I disagree.
Hint: Construct a right-angled triangle with the connecting segment as its hyp
Hint: Construct a right-angled triangle with the connecting segment as its hyp
Chikawakajones
- 22
- 0
tell me step by step...
Tide
Science Advisor
Homework Helper
- 3,072
- 0
It will be the hypotenuse of a triangle whose sides are (14-2)/2 and (14+2)/2.
Last edited:
futb0l
make a triangle using the line as the hypotenuse
side 1:
Get the radius of the big circle and subtract the radius of the small circle. Giving you 7 - 1 = 6
side 2:
Get the radius of the big and the small circle.
Giving you 7 + 1 = 8
Hopefully you can solve the problem now.
side 1:
Get the radius of the big circle and subtract the radius of the small circle. Giving you 7 - 1 = 6
side 2:
Get the radius of the big and the small circle.
Giving you 7 + 1 = 8
Hopefully you can solve the problem now.
Last edited by a moderator:
mahesh_2961
- 20
- 0
let me see ..
draw two lines, one from each center perpendicular to the bottom side (as in the figure ) Then draw a line parallel to the bottom line through the center of the smaller circle.. Then u will see a
right angled triangle formed with hypotenuse being the line connecting the two centers ...
u can now very easiy find the length of thwo sides and hence that of the hypotenuse ..
answer = sqrt (6^2+8^2) = 10
draw two lines, one from each center perpendicular to the bottom side (as in the figure ) Then draw a line parallel to the bottom line through the center of the smaller circle.. Then u will see a
right angled triangle formed with hypotenuse being the line connecting the two centers ...
u can now very easiy find the length of thwo sides and hence that of the hypotenuse ..
answer = sqrt (6^2+8^2) = 10
theriddler876
- 98
- 0
youre making it all more complicated, the center of an inscribed circle is righ in the center of the square so the distance from the center to one side is the half of what the whole length of the square is so you need to square root the areas given to find the lengths divide each length by two, and add them together, the answer should be nine
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
theriddler876 said:youre making it all more complicated, the center of an inscribed circle is righ in the center of the square so the distance from the center to one side is the half of what the whole length of the square is so you need to square root the areas given to find the lengths divide each length by two, and add them together, the answer should be nine
That's simple alright! It just suffers from the minor problem of being wrong.
It would be correct IF the line through the denters were parallel to the sides- but that's not true.
theriddler876
- 98
- 0
hmnn so the squares make more of a stairstep and not a pyramid.
dextercioby
Science Advisor
- 13,388
- 4,042
What pyramid??This is plane geometry...
My answer is
d=\sqrt{106}
The question is:"how did I get that??"
Daniel.
My answer is
d=\sqrt{106}
The question is:"how did I get that??"
Daniel.
dextercioby
Science Advisor
- 13,388
- 4,042
mahesh_2961 said:let me see ..
draw two lines, one from each center perpendicular to the bottom side (as in the figure ) Then draw a line parallel to the bottom line through the center of the smaller circle.. Then u will see a
right angled triangle formed with hypotenuse being the line connecting the two centers ...
u can now very easiy find the length of thwo sides and hence that of the hypotenuse ..
answer = sqrt (6^2+8^2) = 10
Good method,bad answer.
theriddler876 said:youre making it all more complicated, the center of an inscribed circle is righ in the center of the square so the distance from the center to one side is the half of what the whole length of the square is so you need to square root the areas given to find the lengths divide each length by two, and add them together, the answer should be nine
1.Wrong answer,wrong method.
2.There's more common the expression "perimeter of a square".Similar,the"circumference of a circle".
Daniel.
apchemstudent
- 220
- 0
No your answer was wrong... Mahesh's was the right one.dextercioby said:Good method,bad answer...
Daniel.
Here's where you went wrong:
106 = 9^2 + 5^2
wrong numbers. You forgot that the radius of the smaller circle is only 1 not 2.
Thus 7-1 = 6 not 7-2.
As well 7+1 = 8 not 7+2.
I agree with Mahesh's answer...
dextercioby
Science Advisor
- 13,388
- 4,042
Yeah,you're right,sorry,it must be because it's almost 2 am. 
Advice:don't do math at 2 am.
Daniel.

Advice:don't do math at 2 am.
Daniel.
Similar threads
- Replies
- 3
- Views
- 851
- Replies
- 9
- Views
- 2K
- Replies
- 59
- Views
- 1K
- Replies
- 27
- Views
- 1K
- Replies
- 15
- Views
- 1K
- Replies
- 14
- Views
- 2K
- Replies
- 9
- Views
- 1K
- Replies
- 22
- Views
- 3K
- Replies
- 3
- Views
- 2K
- Replies
- 6
- Views
- 1K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math