Calculating the potential of a charged ring

[doktorwho]

1. Homework Statement
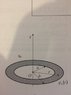
A flat ring, with radii $b>a$ like on the picture is charged with a surface charge density $ρ_s=ρ_0\frac{b}{r}$ where $ρ_0=const.$ Calculate the potential of the ring on the $z-axis$ by taking the reference point to be in the infinity. Picture below.
2. Homework Equations
Since the reference point is in the infinty the expression for the potential is $$dV=\frac{dQ}{4πε_0r}$$

The Attempt at a Solution

I have some ideas and have tried to solve the problem but need the confirmation if this is correct or not.
It goes like this.
1) First i calculated the expression for the total charge on the ring: note: ($ρ_l$ is the linear charge density on one circle of the ring)
$ρ_l=ρ_sdA=ρ_s*rdθ=ρ_s2rπ$
$dQ=ρ_s2rπdr$
2)Then i wrote the expression for the potential: note: ( $R$ is the distance to some point on the $z-axis$
$dV=\frac{dQ}{4πε_0R}$
$V=\int_{a}^{b}\frac{ρ_srdr}{2ε_0\sqrt{z^2+r^2}}$
What do you think about this? Is it correct? Is there an easier way?[/B]

 

[Delta2]

Seems correct to me the final expression for V, cause it is in agreement with what I get if I solve Poisson's equation for the given charge density.

Not sure what you doing when you trying to calculate linear charge density but the expression for dQ seems correct to me also.

 

[Strelkov]

Try starting with the definition of surface charge density:

ρ_{s} dS = dQ

Where S is surface area. You can rewrite:

r = \frac{1}{2} (b + a)

And since the surface area of the ring is simply the difference between the area of the disk defined by b and the disk defined by a, you can quickly obtain an expression for the surface area of the ring. Then, simplifying the result should yield the correct expression for V.

Hope this helps!

- Strelkov