Calculating the V, I and R of resistor components

[marand2017]

Hi there,

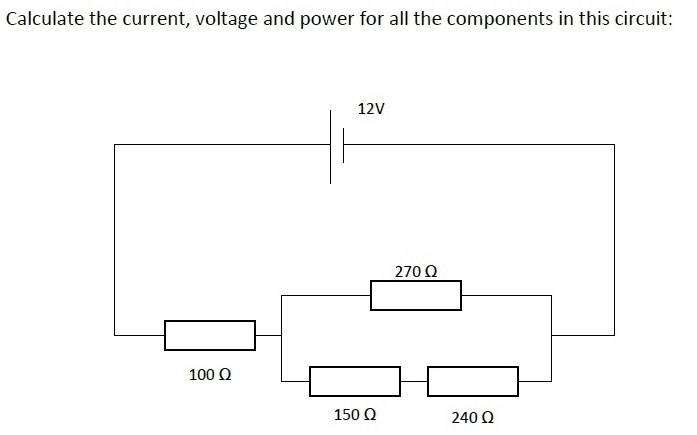The problem asks me to calculate the Voltage, Current and Power of each component within the circuit. I have already calculated the following:

V total = 12 Volts
R total = 259.54 Ohm
I total = 0.046 Amps

I am confused as to how I am supposed to calculate the voltage drop across each resistor. As the circuit contains parallel resistors followed by one in series it is a bit confusing and would greatly appreciate the help. I know how to calculate if all resistors are in parallel or if all are in series but a combination of each is confusing as I need the voltage drop across each resistor.

Thanks

Marco

 

[scottdave]

Do you know how the current flows? How much current is flowing through the 100 Ohm resistor? It is the same as what the battery is delivering.
From that, you can calculate the voltage drop across the 100 Ohm resistor. Subtract that from 12 volts, and you have the voltage drop across the parallel network. Each branch in the parallel network has equal voltage across it. Think of it like water pipes of different diameters, if that helps. The pressure (voltage) at the 'top' of the parallel branch is the same in both branches, but there will be different currents flowing through each branch.
Note that these two currents added together, must equal the total current.

 

[marand2017]

Do you know how the current flows? How much current is flowing through the 100 Ohm resistor? It is the same as what the battery is delivering.
From that, you can calculate the voltage drop across the 100 Ohm resistor. Subtract that from 12 volts, and you have the voltage drop across the parallel network. Each branch in the parallel network has equal voltage across it. Think of it like water pipes of different diameters, if that helps. The pressure (voltage) at the 'top' of the parallel branch is the same in both branches, but there will be different currents flowing through each branch.
Note that these two currents added together, must equal the total current.

Thanks for your prompt reply. I know the Voltage drop over the 100 Ohm Resistor is 4.62 V leaving a voltage drop of 7.38V for the other 3 resistors. However I need to show how much voltage drop there is across each of those 3 resistors. It is not sufficient to consider them as a system.

 

[scottdave]

So you will have 4.62 Volts across the 270 ohm resistor. You also have 4.62 Volts across the series of (150 ohm + 240 ohm = 390 ohm). Calculate the current through 270 ohms. Calculate the current through the 390 ohms. This video may help you understand what is going on.

 

[marand2017]

I have pasted a image of my resolve. I would appreciate any input on it. Thanks.

 

[gneill]

I have pasted a image of my resolve. I would appreciate any input on it. Thanks.

The values that you obtained look okay. You've left out one component though: What is the power associated with the 12 V voltage source? Does the sum of the powers dissipated by the resistors match the power that is associated with the power supply? (That's a good way to check to see if your results are consistent).