Calculating Volume of Cylinder Region w/ X-Y Plane & Theta Angle

[stunner5000pt]

Homework Statement

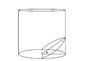
Find the volume of the region bounded by the surface given in the figure.
Until the image is approved this description will have to do.
What is the volume enclosed by the X-Y plane, a cylinder of radius r, and a plane that passes through the center of the cylinder and makes an angle theta with the X-Y plane?

(Hope that was clear enough)

2. The attempt at a solution
Ok since i see a cylinder i think cylindrical coordinates
Is this the correct answer in cylindrical coordinates? Ok i need this problem reformulated in Cartesian because this is for a friend in first year calculus

$$V = \int_{0}^{r} s ds \int_{0}^{\pi} d\phi \int_{0}^{r\cos\theta} dz$$

The reason there is a pi because this is only sweeping half circle. There is a $z\cos \theta$ as upper limit in the z integral because the length of the z varies between zero and $r\cos\theta$.

Is this correct? In cylindrical coordinates? If it is then i can proceed to do it through method of surfaces of revolution in the Cartesian system.

 

[stunner5000pt]

i have revised my solution. The phi integrand was wrong.

I just need someone to tell me if I am right or wrong. Thanks a lot for your help!

 

[stunner5000pt]

bump :)

 

[HallsofIvy]

bump yourself! (I really hate that! If people want to answer your question, they will!)

"What is the volume enclosed by the X-Y plane, a cylinder of radius r, and a plane that passes through the center of the cylinder and makes an angle theta with the X-Y plane?"
passes through the center of the cylinder? Do you mean "Passes through the center of the base of the cylinder in the xy-plane"? That's what your picture shows.
If that is the case, then it looks to me like your integral is correct.

 

[stunner5000pt]

bump yourself! (I really hate that! If people want to answer your question, they will!)

"What is the volume enclosed by the X-Y plane, a cylinder of radius r, and a plane that passes through the center of the cylinder and makes an angle theta with the X-Y plane?"
passes through the center of the cylinder? Do you mean "Passes through the center of the base of the cylinder in the xy-plane"? That's what your picture shows.
If that is the case, then it looks to me like your integral is correct.

now that's what i thought too and the answer i get yields
$$\frac{r^2}{2} * \pi * r\cos\theta$$

but the answer in the textbook is
$$\frac{2}{3}r^3 \cos\theta$$

 

[alpha372]

What book are you using?