Scirel
- 10
- 0
Two identical point charges of q = +1.25 x 10-8 C are separated by a distance of 1.10 m. What is the minimum amount of work required by an external force to move them closer together so that they are only 0.60 m apart?
I have no idea how to do this. I tried using -q(Vb-Va), but that got me 1x10^-6, which is wrong.
The figure below shows three charges at the corners of a rectangle of length x = 0.45 m and height y = 0.29 m. What is the minimum amount of work needed to move the +2.7 µC charge to infinity?
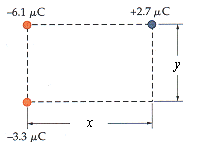
Again, same thing, I tried using that formula, and Vb would be 0 since it is to infinity, but I got -.4779, which is wrong.
I have no idea how to do this. I tried using -q(Vb-Va), but that got me 1x10^-6, which is wrong.
The figure below shows three charges at the corners of a rectangle of length x = 0.45 m and height y = 0.29 m. What is the minimum amount of work needed to move the +2.7 µC charge to infinity?
Again, same thing, I tried using that formula, and Vb would be 0 since it is to infinity, but I got -.4779, which is wrong.