Can Geometry Experts Simplify Complex Proofs?

[ruthless]

Hey,

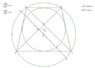
I have this grade 12 Geometry assingment where i have to to prove this question. If there are any smart math ppl out there who are good with geometry please help me. If you r in university or done grade 12 geometery and descrete math then it should be easy for u ... i really need help. I am attaching the question and the diagram i came up with. Please read the question and try to prove it. Thanks a lot. Sorry for the small image sizes as the board has maximum limits please ask me for a bigger version if u need one.

Peace OUt

 

[Chi Meson]

Every geometric proof has a dozen solutions. I see one:

Call the intersection of AD with EF point P
The intersection of DC with EF, point Q

DMP & DSA are similar triangles, as are DMQ & DSC

Can you see how EP : QF is the same proportiality too ?

 

[Chi Meson]

Wait a minute:

AC is NOT parallel to EF is it? Dang!

 

[vsage]

turn the jpg into a monochrome bmp in mspaint and you can crank up the resolution a lot. In the meantime I'm trying to read the question :)

 

[ruthless]

Hey,

Is there any way i can increase the image size and post it here?? For the time being i guess the best thing u guys can do is to zoom the images and try working with them. Thanks a lot for ur help

Bye

 

[ruthless]

Hey,

Chi Meson your idea kinda makes sense to me could you please explain in greater detail how your idea would prove that AS : SC = EM : MF.

Peace

 

[Chi Meson]

Well, it required that AC and EF be parallel, but they aren't. Since they are not, then those triangles I mentioned are not similar. My whole premise fell apart. I can't right away see another solution.

 

[Parth Dave]

Can you tell us what those numbers in the corners are? Because even after zooming they are too foggy to read. Two of them are ratios, but from what to what? And the other two are lengths which i can pick out as being 10.6 cm, correct?

Moving on, I see division of line segments, such that the ratio of AS:SC can be written as t:(1-t) and:
DS = tDA + (1-t)DC

A similar situation for EM:MF is s:(1-s) such that:
DM = sEM + (1-s)MF

I can't make out what numbers you have but in similar problems you would have to find a way to write DM in terms of DS and equate the two. Then write EM and MF in terms of DC and DA. Then you can bring them together and equate them. You'll get something like:
(f1(t, s))DA + (f2(t, s))DC = 0

Since DA and DC are linearly independent the only way this will be true is if f1(t, s) and f2(t, s) are both equal to zero. Then you will have a system of two equations and two unknowns to solve for. At that point you will have to show that t = s and therefore the two are in the same ratio.


But again, I think you will run into a problem with E and F not lying on the quadrilateral. I'm not sure how to resolve that. The solution must have something to do with the inscribed and the circumscribed circles, i just can't see how yet.

 

[ruthless]

Don't worry abt the numbers in the corner ... they do not help with anything ... those were just some calculations i was doing on the side.

 

[nclange27]

Can you possibly get a better resolution for this picture so i can work on it easily
Thnx