sparkle123
- 172
- 0
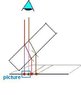
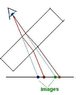
Please see attached. I tried drawing ray diagrams but I don't know how to see the answer intuitively. It seems that there is a relatively simple qualitative proof. Also the angle of incidence is unclear and I think that the direction of the shift depends on this angle.
Thanks!
Thanks!